SOLUTION: The parallel sides of trapezoid ABCD are 3 cm and 9 cm(AB and DC).The non parallel sides are 4 cm and 6 cm(AD and BC).A line(PQ) parallel to base(DC) divides the trapezoid into tw

Note: the word is "perimeter", not "parameteras", as you had it.
"Perimeter" means the distance all the way around a figure.

I corrected that :-)

Here's the trapezoid:



Now we'll draw in PQ parallel to the top and bottom of the trapezoid,
cutting it into two trapezoids with equal perimeters. 


 
Now I'll explain my labeling of those parts:





Divide both sides by 







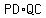
Take reciprocals of both sides



Add 1 to both sides



Replace 1 by 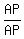 on the left and replace 1 on the right by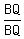 



Combine numerators over denominators:



Since AP+PD = AD = 6 and BQ+QC = BC = 4



Take reciprocals of both sides



Let that ratio be = k



 and 

BQ = 4k,
QC = 4 - 4k
AP = 6k
PD = 6 - 6k 
 
all in centimeters. 
 
Perimeter of the upper trapezoid ABQP:

BQ + AB + AP + PQ

Perimeter of the lower trapezoid PQCD:

QC + DC + PD + PQ

Equating the two perimeters:

BQ + QB + AP + PQ = QC + DC + PD + PQ

Subtract PQ (their common side) from both sides:

     BQ + QB + AP = QC + DC + PD

Substitute their lengths in terms of the fraction k:
 
      4k + 3 + 6k = (4-4k) + 9 + (6-6k)

          10k + 3 = 4 - 4k + 9 + 6 - 6k

          10k + 3 = 19 - 10k
      
              20k = 16

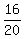                k =  =  = 0.8

Therefore

AP = 6k = 6(0.8) = 4.8 cm.  

BQ = 4k = 4(0.8) = 3.2 cm. 

PD = 6-6k = 6-6(0.8) = 1.2 cm.

QC = 4-4k = 4-4(0.8) = 0.8 cm

We want to find

AP:PD = BQ:QC

which is 4.8:1.2 = 48:12 = 4:1

and checking:

BQ:QC = 3.2:0.8 = 32:8 = 4:1

That's the answer 4:1

Incidentally, the figures above are drawn approximately to scale.
Measure them with a ruler and you will see they are fairly close to
3cm, 4cm, 9cm and 6cm.
  
The perimeters are equal even though the upper trapezoid is obviously 
lots bigger in area.  This demonstrates the important fact that two
figures can have the same perimeter and quite different areas.  

Edwin