Question 319800: Find the coordinates of the center of the circle and length of the radius given the equation of that circle which is 
Found 2 solutions by stanbon, Edwin McCravy:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the coordinates of the center of the circle and length of the radius given the equation of that circle which is 5x^2+15x+5y^2-10y-10=0
----------------------------
Divide thru by 5 to get:
x^2 + 3x + y^2 - 2y - 2 = 0
----
Complete the square on the x-terms and on the y-terms:
---
x^2+3x + (3/2)^2 + y^2 - 2y + 1 = 2 + (3/2)^2 + 1
---
Factor and simplify:
(x+(3/2))^2 + (y-1)^2 = 21/4
----------------
Center: (-3/2 , 1)
Radius: (1/2)sqrt(21)
=========================
Cheers,
Stan H.
=============
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
We need to get it in the form  so we'll
know it has center (h,k) and radius r.
First we add 10 to both sides to get the constant off the left side: so we'll
know it has center (h,k) and radius r.
First we add 10 to both sides to get the constant off the left side:
 Next we divide through by the common coefficient of x² and y² which
is 5
Next we divide through by the common coefficient of x² and y² which
is 5

 Put the addition of one blank after the 3x and another after the -2y since we
are going to add something to both sides
Put the addition of one blank after the 3x and another after the -2y since we
are going to add something to both sides
 Next we calculate what goes in the first blank:
1. Multiply the coefficient of x, which is 3, by
Next we calculate what goes in the first blank:
1. Multiply the coefficient of x, which is 3, by  }, getting }, getting  2. Square that value:
2. Square that value:  , so , so 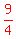 is what goes
in the first blank, and we also add it to the right side: is what goes
in the first blank, and we also add it to the right side:
 Next we calculate what goes in the second blank:
1. Multiply the coefficient of y, which is -2, by
Next we calculate what goes in the second blank:
1. Multiply the coefficient of y, which is -2, by  }, getting }, getting  2. Square that value:
2. Square that value:  , so , so 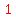 is what goes
in the second blank, and we also add it to the right side: is what goes
in the second blank, and we also add it to the right side:
 The first three terms on the left
The first three terms on the left 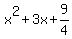 factors as factors as  or or 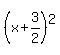 The last three terms on the left
The last three terms on the left 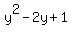 factors as factors as 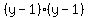 or or 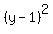 The right side
The right side 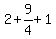 becones becones  So we now have:
So we now have:
 And we compare that to
And we compare that to
 and we see that since
and we see that since  , ,  , and
since , and
since  , ,  . Also . Also  so so  }
Edwin }
Edwin .
|
|
|