Question 311575: The sum of the lengths of any two sides of a triangle must be greater than the third side. If a triangle has one side that is 18cm and a second side that is 3cm less than twice the third side, what are the possible lengths for the second and third sides?
Answer by Edwin McCravy(20066)   (Show Source): (Show Source):
You can put this solution on YOUR website! The sum of the lengths of any two sides of a triangle must be greater than the third side. If a triangle has one side that is 18cm and a second side that is 3cm less than twice the third side, what are the possible lengths for the second and third sides?
The three sides are:
First side = 18
Third side = x
Second side = 2x - 3
First side + Second side > Third Side, therefore 18 + (2x - 3) > x
First side + Third side > Second Side, therefore 18 + x > 2x - 3
Second side + Third side > Second Side, therefore (2x - 3) + x > 18
So we have:
 Simplifying:
Simplifying:
 Simplifying further:
Simplifying further:
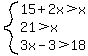 Simplifying further:
Simplifying further:
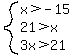 Simplifying further:
Simplifying further:
 We can eliminate the first inequality, since the third one guarantees it
because if x is greater than 7 it is CERTAILY greater than =15.
We can eliminate the first inequality, since the third one guarantees it
because if x is greater than 7 it is CERTAILY greater than =15.
 Those two inequalities can be combined as
Those two inequalities can be combined as
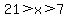 or if we prefer:
or if we prefer:
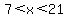 , which is the same thing.
So the third side, x, is greater than 7 but less than 21.
Since the Second side is 2x - 3, we must build 2x - 3
from the x which is in the middle of , which is the same thing.
So the third side, x, is greater than 7 but less than 21.
Since the Second side is 2x - 3, we must build 2x - 3
from the x which is in the middle of 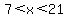 .
To make the x into a 2x, we multiply all three sides of .
To make the x into a 2x, we multiply all three sides of
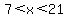 by 2, getting by 2, getting
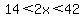 ,
To make the 2x into a 2x - 3, we subtract 3 from all three sides of the above: ,
To make the 2x into a 2x - 3, we subtract 3 from all three sides of the above:
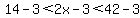 Simplifying
Simplifying
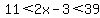 So
So 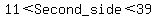 So the Second side, 2x - 3, is greater than 11 but less than 39.
Edwin
So the Second side, 2x - 3, is greater than 11 but less than 39.
Edwin
|
|
|