SOLUTION: The lengths of the sides of a triangle are 13, 13, and 10. The circumscribed circle of a triangle is a circle that goes through each of the three vertices of the triangle and has i

 
We start with this triangle ABC
 


where AC = BC = 13, and AB = 10


The circumcenter (center of the circumscribed circle)
is the point where the perpendicular bisectors of
the sides meet.  Let D be the midpoint of AB, and
E be the midpoint of BC.  Since the triangle is
isosceles CD is the perpendicular bisector of AB.

Then we draw EO perpendicular to BC, and EO is the
perpendicular bisector of BC.  So point O is the
circumcenter.


 
We can now draw the circumscribed circle with
center O and radius OC.



We need to calculate the length of the radius OC.

Since BC = 13, then CE =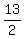  

Triangle CEO is similar to triangle ACD, so

we have the proportion:



Since BC = 13, then CE = 

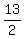AC is given = 13

Since AB = 10, AD = 5, 

By the Pythagorean theorem:











Now the proportion



becomes:



Simplifying the compound fraction on the right
by multiplying top and bottom by 2



The proportion is now:



Cross-multiplying:





So the radius of the circumscribed circle is 

-----------------

However, there is a false statement in your problem. It states

The circumscribed circle of a triangle is a circle that goes 
through each of the three vertices of the triangle and has its 
centre inside the triangle.

It is not true that the circumscribed circle always has its
center inside the triangle.  It is in your particular
problem above. However, here is a case where the center of the
circumscribed circle of a triangle is OUTSIDE the triangle:



Edwin