SOLUTION: For how many integer values of x does there exist a triangle whose sides have length 2 1/2, 5, and x ?

In any triangle, the sum of any two sides must be greater
than the third side.

That is, these three inequalities must hold:



The third inequality is bound to hold, since regardless
of what positive integer x is the left side is larger
than 5 so obviously it's larger than .

So we only need to concentrate on the first two inequalities.

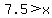The first inequality abounts to  and the second
inequality, when solved for x amounts to .

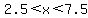Thus x is an integer such that  and the only
integers between 2.5 and 7.5 are 3,4,5,6,and 7.

So those are the only integers x can take on.  The answer is 5.

Edwin