SOLUTION: turn into the variable the length of a rectangle is twice its width if the width is increased by one meter and the length is diminished by three meters the area will be 12 square m

Algebra ->  Customizable Word Problem Solvers  -> Geometry -> SOLUTION: turn into the variable the length of a rectangle is twice its width if the width is increased by one meter and the length is diminished by three meters the area will be 12 square m      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 224003: turn into the variable the length of a rectangle is twice its width if the width is increased by one meter and the length is diminished by three meters the area will be 12 square meters
Answer by drj(1380) About Me  (Show Source):
You can put this solution on YOUR website!
Turn into the variable the length of a rectangle is twice its width if the width is increased by one meter and the length is diminished by three meters the area will be 12 square meters.

I assume you want the original dimensions of the rectangle.

Step 1. Let w be the width.

Step 2. Let 2w be the length.

Step 3. Let w+1 be the width increase by 1.

Step 4. Let 2w-3 be the length increase by 3 meters.

Step 5. Area A=(w+1)(2w-3)=12. Solving yields the following steps

%28w%2B1%29%282w-3%29=12

2w%5E2-3w%2B2w-3=12

2w%5E2-w-3=12

Subtract 12 from both sides of the equation to get a quadratic equation

2w%5E2-w-3-12=12-12%7D%7D%0D%0A%0D%0A%0D%0A%7B%7B%7B2w%5E2-w-15=0

Step 6. To solve, use the quadratic formula given as

w+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+

where a=2, b=-1, and c=-15.

Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation aw%5E2%2Bbw%2Bc=0 (in our case 2w%5E2%2B-1w%2B-15+=+0) has the following solutons:

w%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-1%29%5E2-4%2A2%2A-15=121.

Discriminant d=121 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--1%2B-sqrt%28+121+%29%29%2F2%5Ca.

w%5B1%5D+=+%28-%28-1%29%2Bsqrt%28+121+%29%29%2F2%5C2+=+3
w%5B2%5D+=+%28-%28-1%29-sqrt%28+121+%29%29%2F2%5C2+=+-2.5

Quadratic expression 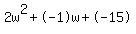2w%5E2%2B-1w%2B-15 can be factored:
2w%5E2%2B-1w%2B-15+=+2%28w-3%29%2A%28w--2.5%29
Again, the answer is: 3, -2.5. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+2%2Ax%5E2%2B-1%2Ax%2B-15+%29



Choosing the positive solution, w=3, then 2w=6. The changed dimensions gives an area A=(3+1)(6-3)=12 which is a true statement base on the problem.

Step 7. ANSWER: The dimensions of the rectangle is 3 meters and 6 meters.

I hope the above steps and explanation were helpful.

For Step-By-Step videos on Introduction to Algebra, please visit http://www.FreedomUniversity.TV/courses/IntroAlgebra and for Trigonometry please visit http://www.FreedomUniversity.TV/courses/Trigonometry.

Also, good luck in your studies and contact me at john@e-liteworks.com for your future math needs.

Respectfully,
Dr J

http://www.FreedomUniversity.TV