Question 176361: A farmer decides to enclose a rectangular garden, using the side of a barn as one side of the rectangle. What is the maximum area that the farmer can enclose with 100ft of fence? What should the dimensions of the garden be to give this area?
Please help I have never been good with word problems.
Thank you
Answer by josmiceli(19441)   (Show Source):
You can put this solution on YOUR website! Since 1 side is the barn, the farmer needs only 3 sides.There will
be 2 equal length sides perpendicular to the barn and one side parallel
to the barn.
Let  = the length of a side perpendicular to barn
Let  = the length of the side parallel to the barn
Let  = the area enclosed by the fencing
Given:
--------------
 formula for the area of a rectangle
And, from above,
This is a function 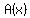 . I can plot it and find the
maximum. I also know that, given a general equation
 , there is a maximum if the sign of
 is negative. That maximum occurs at
 . In this case,
 ft
When  ,
 ft
 ft2
I'll plot the equation A(x), too
A good way to check to see if you have a maximum is
to just tweak the numbers a tiny bit, like
 What's the area?
 The area went down as it should
Then tweak the other way
area also went down
So, 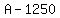 looks like a maximum
|
|
|
