Question 159823This question is from textbook
: A square piece of cardboard is formed into a box by cutting out 2-inch squares from each of the corners and folding up the sides. If the volume of the box needs to be 84.5 cubic inches, what size square piece of cardboard is needed?
This question is from textbook
Found 2 solutions by checkley77, Earlsdon:
Answer by checkley77(12844)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let x=the sides of the square piece of cardboard.
Cutting a 2 in. square out of each corner leaves the base measurements:
(x-4)^2=x^2-8x+16
The height is 2 in.
volume=2(x^2-8x+16)
84.5=2x^2-16x+32
2x^2-16x+32-84.5=0
2x^2-16x-52.5=0
(x-10.5)(x+2.5)=0
x-10.5=0
x=10.5 inches is the original side of the piece of square cardboard.
Proof:
84.5=2(10.5^2-8*10.5+16)
84.5=2(110.25-84+16)
84.5=2*42.25
84.5=84.5
Answer by Earlsdon(6294)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the size of the square piece of cardboard be x by x inches.
If you cut 2-inch squares from each of the four corners, the sides now measure (x-4) inches, and this will be the measure of the sides of the base of the newly-formed box.
The volume of a rectangular (s by s square base) prism with a height of h is given by:
 and, in this problem, s = (x-4) and h = 2, so... and, in this problem, s = (x-4) and h = 2, so...
 and this is to be 84.5 cu.in. and this is to be 84.5 cu.in.
So we have enough information to set up the equation in x.
 Performing the indicated multiplication, we get: Performing the indicated multiplication, we get:
 Subtracting 84.5 from both sides, we have: Subtracting 84.5 from both sides, we have:
 Use the quadratic formula to solve this trinomial: Use the quadratic formula to solve this trinomial:  where: a = 2, b = -16, and c = -52.5. where: a = 2, b = -16, and c = -52.5.
Making the appropriate substitutions, we get:
 Simplifying this, we get: Simplifying this, we get:


 or or 
 or or  Discard the negative solution as the sides of the box are positive, so we end up with: Discard the negative solution as the sides of the box are positive, so we end up with:
 inches. This is the size of the original square piece of cardboard. inches. This is the size of the original square piece of cardboard.
Let's check the solution:
 = = = = 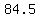 OK! OK!
|
|
|