SOLUTION: Find the dimensions of a rectangle whose perimeter is 26 meters and whose area is 40 square meters.

Algebra ->  Customizable Word Problem Solvers  -> Geometry -> SOLUTION: Find the dimensions of a rectangle whose perimeter is 26 meters and whose area is 40 square meters.      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 159731: Find the dimensions of a rectangle whose perimeter is 26 meters and whose area is 40 square meters.
Found 2 solutions by KnightOwlTutor, jojo14344:
Answer by KnightOwlTutor(293) About Me  (Show Source):
You can put this solution on YOUR website!
We know that the perimeter is equal to the length of all the sides
X=width
Y=length
The perimeter of the rectangle=X+X+Y+Y=26
Simplify to 2X+2Y=26
we know that the area is the width multplied by the length
XY=40
We isolate X by dividing Y on both sides X=40/Y
Replace 40/Y for X in the perimeter equation
2(40/Y) +2Y=26
Multiply each term on both sides by Y
80+2Y^2=26Y
subtract 26Y from both sides
80-26Y+2Y^2=0
This is a quadratic equation
Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc)
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 2x%5E2%2B-26x%2B80+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-26%29%5E2-4%2A2%2A80=36.

Discriminant d=36 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--26%2B-sqrt%28+36+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%28-26%29%2Bsqrt%28+36+%29%29%2F2%5C2+=+8
x%5B2%5D+=+%28-%28-26%29-sqrt%28+36+%29%29%2F2%5C2+=+5

Quadratic expression 2x%5E2%2B-26x%2B80 can be factored:
2x%5E2%2B-26x%2B80+=+%28x-8%29%2A%28x-5%29
Again, the answer is: 8, 5. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+2%2Ax%5E2%2B-26%2Ax%2B80+%29

Answer by jojo14344(1513) About Me  (Show Source):
You can put this solution on YOUR website!

First P=2%28L%2BW%29
26=2%28L%2BW%29 ------> cross%2826%2913%2Fcross%282%29=cross%282%29%28L%2BW%29%2Fcross%282%29
L%2BW=13
L=13-W, EQN 1
And,
A=L%2AW, substitute EQN 1
40=%2813-W%29%28W%29
40=13W-W%5E2
W%5E2-13W%2B40=0, perfect square, can be factor out
%28W-5%29%28W-8%29=0
2 values, either,
W%5B1%5D=5m, or W%5B2%5D=8m
Get L via EQN 1:
L%5B1%5D=13-W%5B1%5D=13-5=8m, and L%5B2%5D=13-W%5B2%5D=13-8=5m
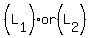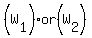
Go back Perimeter and Area to check: use either %28L%5B1%5D%29or%28L%5B2%5D%29 or %28W%5B1%5D%29or%28W%5B2%5D%29
1) P=2%28L%5B1%5D%2BW%5B1%5D%29
26m=2%288%2B5%29=2%2813%29
26m=26m
2) A=L%5B1%5D%2AW%5B1%5D
40m%5E2=%288m%29%285m%29
40m%5E2=40m%5E2
Thank you,
Jojo