Question 151799: A dog owner has 250 feet of fencing to enclose a rectangular run for his dogs. If he wants the maximum possible area, what should the length and width of the rectangle be?
Answer by Earlsdon(6294)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's start with the formulas for the area and the perimeter of a rectangle.


The perimeter is given as 250 feet, so we can write:
 Dividing both sides by 2, we get: Dividing both sides by 2, we get:
 Rewrite this as: Rewrite this as:
 and substitute it into the formula for the area (A = L*W), and substitute it into the formula for the area (A = L*W),
 Simplifying this, we get: Simplifying this, we get:
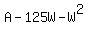 Now this is a quadratic equation and if you were to graph this, you see a parabola that opens downward, thus there would be a maximum value of A (also known as the vertex). Now this is a quadratic equation and if you were to graph this, you see a parabola that opens downward, thus there would be a maximum value of A (also known as the vertex).
You can find the value of W at this vertex by:
 This comes from the standard form for a quadratic equation: This comes from the standard form for a quadratic equation:
In this problem, a = -1 and b = 125, so, making the appropriate substitutions, we get:

 Now this is the value of W (the width) that would make the area (A) a maximum. Now this is the value of W (the width) that would make the area (A) a maximum.
The length (L) is:



So the length and the width of the rectangle would be L = 62.5 feet and W = 62.5 feet. In other words, the rectangle is a square.
|
|
|