Question 134386: How many times might a circle and a square intersect?
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
First we know that, by definition, a 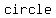 is a plane with is a plane with 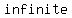 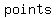 from its radius and a from its radius and a 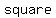 is a is a  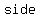  with with  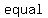 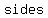 . .
 there were there were    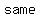  , then these two figures would intersect each other , then these two figures would intersect each other 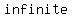 times because a circle is a set of all points on the plane. times because a circle is a set of all points on the plane.
Can a circle and square intersect in exactly one point?
I think that it is certainly possible to have a circle and square intersect in one point, and furthermore, I think this can happen in three main ways:
If the square is outside the circle:
- a case of 1 side tangential
- case of 1 corner touching
-if the square is outside the circle: in this case, we only can have 1 corner touching
Can a circle and square intersect in exactly two points?
I do think we can intersect a square with a circle in exactly two points, and I have determined there to be four main ways:
-if three vertices inside the circle
-if two vertices inside the circle
-if one vertex inside the circle
-if no vertices inside the circle
Can a square and a circle intersect in exactly  points for each points for each  = =  , ,  , ... , ... ,…… ,……
If you analyze these cases, you will see that only possible solutions are that a square and circle can intersect in  , , , , , or , or  times-depends on the size and position of the shapes. times-depends on the size and position of the shapes.
|
|
|