We can't tell which rectangle is given as a golden rectangle. Plus, you
didn't tell us what " a ", and what, if anything, you are letting be 1.
Probably English is not your first language. That is OK!! It is my ONLY
language. J
 I will assume that rectangle ACDF is given as a golden rectangle, and I will
assume that the length of a side of square ABEF is " a ". the shorter side of
rectangle BCDE is given as " 1 ".
By definition of 'golden rectangle':
I will assume that rectangle ACDF is given as a golden rectangle, and I will
assume that the length of a side of square ABEF is " a ". the shorter side of
rectangle BCDE is given as " 1 ".
By definition of 'golden rectangle':
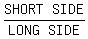


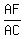


Rectangle BCDE is similar to rectangle ACDF.



a. Show that
(a/1) = 1/(a - 1)


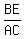
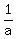

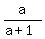 CROSS-MULTIPLY
CROSS-MULTIPLY


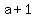
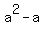

 <-- use this in part (b)
<-- use this in part (b)


 Divide both sides by (a-1)
Divide both sides by (a-1)
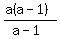

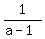
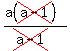

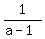
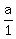

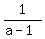
b. Find the exact value of a(which will give you the golden ratio) by completing the square.
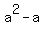

 1. Get half of coefficient of a: (-1)/2 = -1/2
2. Square (-1/2), get +1/4
3. Add to both sides
1. Get half of coefficient of a: (-1)/2 = -1/2
2. Square (-1/2), get +1/4
3. Add to both sides
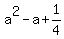

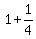 Factor left side into the square of a binomial:
Factor left side into the square of a binomial:
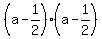




 Take square roots of both sides, using ± on right.
Take square roots of both sides, using ± on right.


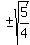
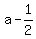

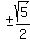


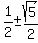


 Since ' a ' is not negative, we discard the - sign:
Since ' a ' is not negative, we discard the - sign:


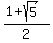 That is the exact value of ' a ', the golden ratio.
Edwin
That is the exact value of ' a ', the golden ratio.
Edwin