Question 1207915: In 2008, the Singapore Flyer opened as the world’s largest Ferris wheel. It has a maximum height of 165 meters and a diameter of 150 meters,with one full rotation taking approximately 30 minutes. Find an equation for the wheel if the center of the wheel is on the y-axis.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
.
In 2008, the Singapore Flyer opened as the world’s largest Ferris wheel.
It has a maximum height of 165 meters and a diameter of 150 meters,
with one full rotation taking approximately 30 minutes.
Find an equation for the wheel if the center of the wheel is on the y-axis.
~~~~~~~~~~~~~~~~~
The radius of the wheel is half of its diameter, i.e. 150/2 = 75 meters.
The center of the wheel is at the height of 165-75 = 90 meters over the ground.
The problem does not tells, which coordinate system to use; so, I will chose
the system at the ground level.
In this system, the center of the wheel is the point with coordinates (0,90) meters.
So, in standard equation of a circle
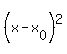 + + 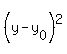 = r^2,
where ( = r^2,
where ( , , ) is the center, "r" is the radius, we should take ) is the center, "r" is the radius, we should take
 = 0, = 0,  = 90, r = 75.
Thus, the equation of this wheel is = 90, r = 75.
Thus, the equation of this wheel is
 + + 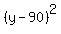 = = 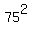 ,
or ,
or
 + + 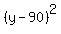 = 5625. = 5625.
Solved.
----------------
In this problem, the information about the rate of rotation
(the duration of one rotation) is irrelevant to the question.
A TWIN problem was solved at this forum yesterday under this link
https://www.algebra.com/algebra/homework/word/geometry/Geometry_Word_Problems.faq.question.1207910.html
|
|
|