Question 1207601: An open box is to be constructed from a square piece of sheet metal by removing a square of side 1 foot from each corner and turning up the edges. If the box is to hold 5 cubic feet, what should be the dimension of the sheet metal?
Note: This is a popular problem found in many textbooks but I haven't found one decent explanation. Can someone solve this application one step at a time?
Found 3 solutions by ikleyn, Theo, MathTherapy:
Answer by ikleyn(52946)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
An open box is to be constructed from a square piece of sheet metal by removing a square of side 1 foot
from each corner and turning up the edges. If the box is to hold 5 cubic feet, what should be the dimension
of the sheet metal?
Note: This is a popular problem found in many textbooks but I haven't found one decent explanation.
Can someone solve this application one step at a time?
~~~~~~~~~~~~~~~~~~~~~~~~~~
When we turn up the edges, we will get an open box with a square base,
and the height of the box will be exactly one foot.
Since the box is to hold 5 cubic feet, it means that the base area is 5 square feet.
Hence, the size of the square bottom is  sq.feet (or about 2.236 ft) in each direction.
Now take into account 1 ft edges, turned up.
It means that the size of the original squared piece of metal is sq.feet (or about 2.236 ft) in each direction.
Now take into account 1 ft edges, turned up.
It means that the size of the original squared piece of metal is 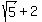 ft in each direction.
ANSWER. The original piece of metal is a square with the side length of ft in each direction.
ANSWER. The original piece of metal is a square with the side length of 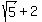 ft in each direction. ft in each direction.
Solved, with all necessary explanations.
-----------------
In order for my work didn't go to waste, please answer my questions:
(a) Do you understand my explanations and logic ?
(b) Is this solution and explanations useful to you ?
(c) In your view, is this a descent solution ?
As a conclusion, you may express your " THANKS " to me for my teaching.
When you answer these questions, I will post to you the links to the lessons,
containing many other solutions to similar problems.
///////////////
When I read the post by @Theo, I see several deficiencies.
First, @Theo systematically writes sentences like this "side of the square piece of sheet metal be (x+2)",
but does not attach the dimension of feet to it. Every time, it makes an impression of incomplete sentence.
Also, in his post @Theo systematically refers to 1 inch, while the dimension to refer
in this problem is 1 foot. Every time, it produces confusion in the head of a reader.
Also, the general style of writing suffers of permanent repeating of the same idea
and heavy tautology. Read, for example, this typical example/statement
"since the length of the square piece of sheet metal is equal to x + 2,
and the width of the square piece of sheet metal is also equal to x + 2,
then both the length and the width of the square piece of sheet metal are equal to sqrt(5) + 2."
Common sense, the rules of writing (and Math writing, in particular), as well as the sense of harmony
all do recommend to avoid such speculations so as not to bore the reader.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! let the length of a side of the square piece of sheet metal be (x + 2).
the area of the square piece of sheet metal is (x + 2) ^ 2 = x^2 + 4x + 4.
the length is (x + 2) and the width is (x + 2), because the length equals the width of a square.
if you take a square inch off each corner, then you are taking 1 inch off the length on each corner and you are taking 1 inch off the width on each corner.
what you are left with is a length of x and a width of x 4 flaps on each side that each have a length of x and a width of 1.
when you fold up these flaps, you have a box that has a length of x and a width of x and a height of 1.
the volume of this box is equal to 5.
volume is equal to length * width * height.
this becomes x * x * 1 = 5
this becomes x^2 = 5 which gets you x = plus or minus sqrt(5).
the original measure of the square piece of metal are (x + 2).
this means the measure of the original length of the box is 2 + sqrt(5) and the measure of the original width of the box is 2 + sqrt(5).
the area of the box is therefore equal to (2 + sqrt(5)) ^ 2 - 17.94427191 square feet.
here's my diagram.
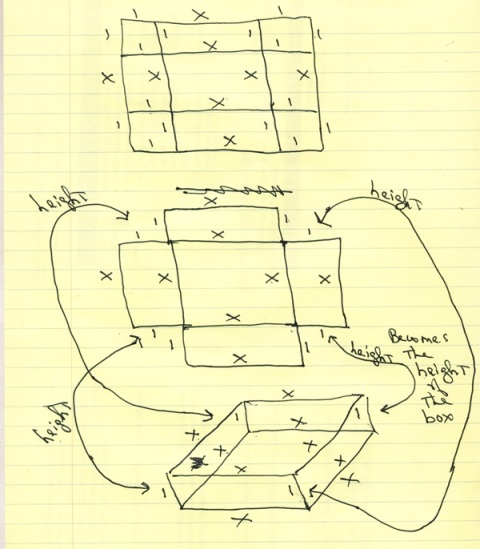
the top diagram shows the square piece of sheet metal with 1 square inch marked on each corner.
the length of the square piece of sheet metal becomes x + 2 and the width of the square piece of sheet metal becomes x + 2 as well.
in the middle diagram, a 1 inch square piece of sheet metal has been removed from each corner.
what you are left with is an inner square with length equal to x and width equal to x and 4 flaps, each of which contains a length of 1 and a width of x.
in the bottom diagram, the flaps have been folded up to form the box.
the length of each flap becomes the height of the box.
the box has a length of x and a width of x and a height of 1.
the volume of this box is given as 5 cubic feet.
since the volume of the box is equal to length * width * height, then the volume of the box is equal to x * x * 1 which is equal to x^2 which is equal to 5.
if you solve for x, you will bet x = plus or minus sqrt(5).
since the length of the square piece of sheet metal is equal to x + 2, and the width of the square piece of sheet metal is also equal to x + 2, then both the length and the width of the square piece of sheet metal are equal to sqrt(5) + 2.
your solution should be that the length of each side of the square piece of sheet metal is equal to sqrt(5) + 2 which is roughly equal to 4.236067977.
i checked the solution several times and am reasonably confident it's accurate.
let me know if this works for you.
theo
Answer by MathTherapy(10559)   (Show Source): (Show Source):
You can put this solution on YOUR website!
An open box is to be constructed from a square piece of sheet metal by removing a square of side 1 foot from each corner and turning up the edges. If the box is to hold 5 cubic feet, what should be the dimension of the sheet metal?
Note: This is a popular problem found in many textbooks but I haven't found one decent explanation. Can someone solve this application one step at a time?
Since the dimensions of the sheet metal are being sought, we let the width, which is also the same measure as
the length (the sheet metal is SQUARE), be W
As a 1-foot square piece is removed from each end of the sheet metal, the width and the length of the base/bottom
of the box will be W - 2, each.
The sides/height of the box will be formed from the 1-foot cut-outs
So, as the open box will have a volume (Length * Width * Height, or LWH) of 5 cubic feet, we get:
L*W*H = 5. Now, with W (width) = W - 2 (same measure as the length, or L), LWH = 5 becomes:
(W - 2)(W - 2)(1) = 5
(W - 2)2 = 5
W2 - 4W + 4 = 5
W2 - 4W - 1 = 0
As the above quadratic cannot be factored with INTEGERS, solutions can be derived by using the quadratic equation
formula or completing the square. Using the former, we get: 
 , with , with 
 Width/Length of sheet metal, or
Width/Length of sheet metal, or  or or  <=== IGNORE/REJECT as
length|width CANNOT be negative (<0)
Dimensions of sheet metal: <=== IGNORE/REJECT as
length|width CANNOT be negative (<0)
Dimensions of sheet metal: 
|
|
|