Question 1199587: Alpha particles are deflected along the hyperbolic paths when they
are directed towards the nuclei of gold atoms. If an alpha particle
gets as close as 12 units to the nucleus along the hyperbolic path
with asymptotes of 𝑦=5x/12, what is the equation of its path.
Assume that the transverse axis is on y-axis. Illustrate the said path
taken by the alpha particles. Illustrate the path taken by the alpha
particles.
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Alpha particles are deflected along the hyperbolic paths when they
are directed towards the nuclei of gold atoms. If an alpha particle
gets as close as 12 units to the nucleus along the hyperbolic path
with asymptotes of 𝑦 = 5x/12, what is the equation of its path.
Assume that the transverse axis is on y-axis. Illustrate the said path
taken by the alpha particles. Illustrate the path taken by the alpha
particles.
~~~~~~~~~~~~~~~~~~~~~
First of all, the problem formulation in the post has an error, which SHOULD be FIXED.
The problem talks about asymptotes (plural), but shows only one asymptote y = 5x/12.
Actually, from the context, there are TWO asymptotes y = +/- 5x/12.
Secondly, before to start the solution, this Physics context must be translated to Math problem.
This translation is as follows.
Find a hyperbola equation based on following properties:
- the asymptotes are y = +/- 5x/12;
- the transverse axis is y-axis;
- one of the vertex of the hyperbola is y= 12 units at x= 0.
Having this translation, the solution is easy.
Since the asymptotes are
y = 5x/12 and y = -5x/12 and since the transverse axis is y-axis,
the equation of the hyperbola has the form
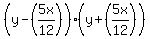 = const,
where const is some constant value, now unknown.
We determine this constant value from the condition y = 12 at x= 0, which gives = const,
where const is some constant value, now unknown.
We determine this constant value from the condition y = 12 at x= 0, which gives
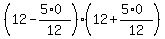 = const,
const = = const,
const =  = 144.
Thus, the hyperbola equation is = 144.
Thus, the hyperbola equation is
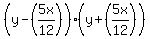 = =  ,
or, equivalently ,
or, equivalently
 - - 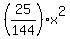 = =  , ,
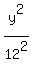 - - 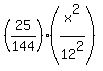 = 1. = 1.
Solved.
|
|
|