Question 1195557: A candy company wants to reduce the amount of packaging they use, by minimizing the
surface area. If they still want the candy package to hold a volume of 250 cm3, what is the
minimum surface area? Assume the candy comes packaged in rectangular prisms. Round to
one decimal place.
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A candy company wants to reduce the amount of packaging they use, by minimizing the
surface area. If they still want the candy package to hold a volume of 250 cm3, what is the
minimum surface area? Assume the candy comes packaged in rectangular prisms. Round to
one decimal place.
~~~~~~~~~~~~~~~~~~~~~~~
Let x, y and z be the dimensions of a rectangulas prism.
Then its volume is
xyz = 250 cm^3, (1)
a fixed value, and the problem wants we minimize the surface area 2xy + 2yz + 2xz under this restriction (1).
It is the same as to minimize the function of 3 independent variables
F(x,y,z) = xy + yz + xz
under restriction (1).
Using the restriction, we can reduce function F(x,y,z) to function of two independent variables
f(x,y) = xy + 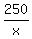 + + 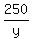 and look for the minimum of this function.
To find its minimum, we take partial derivatives of f(x,y) over x and y and equate them to zero.
It gives us this system of equations
y -
and look for the minimum of this function.
To find its minimum, we take partial derivatives of f(x,y) over x and y and equate them to zero.
It gives us this system of equations
y - 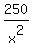 = 0, (2) (x-derivative)
x - = 0, (2) (x-derivative)
x - 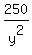 = 0. (3) (y-derivative)
From (2) and (3)
x^2*y = 250 (4)
x*y^2 = 250. (5)
Dividing (4) by (5), we get = 0. (3) (y-derivative)
From (2) and (3)
x^2*y = 250 (4)
x*y^2 = 250. (5)
Dividing (4) by (5), we get
 = 1, or x = y.
Working similarly with the other pair of independent variables, we can get similarly x = z,
which tells us that the minimum surface value is achieved for the cube x = y = z.
Its dimension is = 1, or x = y.
Working similarly with the other pair of independent variables, we can get similarly x = z,
which tells us that the minimum surface value is achieved for the cube x = y = z.
Its dimension is  = 250, or x = = 250, or x =  = 6.3 (rounded to one decimal place).
ANSWER. The minimum surface area rectangular prism is a cube with the edge size of = 6.3 (rounded to one decimal place).
ANSWER. The minimum surface area rectangular prism is a cube with the edge size of  = 6.30 cm.
Its surface area is = 6.30 cm.
Its surface area is 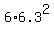 = 238.1 cm^2 (rounded to one decimal place).
CHECK. = 238.1 cm^2 (rounded to one decimal place).
CHECK. 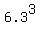 = 250.047 cm^3. = 250.047 cm^3.
Solved, answered and explained.
---------------
Do not forget to post your "THANKS" to me for my teaching.
|
|
|