Question 1194944: if x is the set of multiples of 5, and Y is the set of three-digit positive integers which are multipels of 7, how many numbers are common to both sets
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52780)   (Show Source):
You can put this solution on YOUR website! .
if x is the set of multiples of 5, and Y is the set of three-digit positive integers
which are  multiples of 7, how many numbers are common to both sets
~~~~~~~~~~~~~~~~~
First such number is 105, and then every 35-th integer number in this sequence of natural numbers
106, 107, 108, . . . , 998, 999
satisfies the criterion.
So, you calculate this ratio
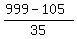 = 25.54...
as a decimal, and then you round this decimal to the closest smaller integer, which is 25.
Doing this way, you determine the number of segments of the length of 35 units from 106 to 999.
Each such segment contains one and only one integer number multiple of 5 and 7 simultaneously
as the last number of the segment.
Finally add 1 (one), which counts for the number of 105.
So, your answer is 25 + 1 = 26.
Solved and explained.
Answer by math_tutor2020(3816)  (Show Source):
You can put this solution on YOUR website!
X = multiples of 5
X = {5, 10, 15, ...}
100 is the smallest three-digit number
100/7 = 14.2857 approximately which rounds up to 15
7*14 = 98 is too small
7*15 = 105 clears the threshold showing that 105 is the smallest three-digit number that's a multiple of 7
999 is the largest three-digit number
999/7 = 142.714 approximately
142*7 = 994
143*7 = 1001 is too big
So 994 is the largest three-digit number that's a multiple of 7
Y = multiples of 7 that are three-digit numbers
Y = {105, 112, 119, ..., 987, 994}
Y = {7*15, 7*16, 7*17, ..., 7*141, 7*142}
Z = set of numbers in BOTH set X and set Y
Z = multiples of 5 and multiples of 7 that are 3 digits
Z = multiples of 35 (aka 5*7) that are 3 digits
Z = {105, 140, 175, ..., 945, 980}
Z = {3*35, 4*35, 5*35, ..., 27*35, 28*35}
Notes:
100/35 = 2.857 approximately to help locate the smallest three-digit multiple of 35 (round up)
999/35 = 28.54 approximately; this helps spot the largest three-digit multiple of 35 (round down)
Anyways, we have this set
Z = {3*35, 4*35, 5*35, ..., 27*35, 28*35}
Focus on the numbers up front
{3, 4, 5, ..., 27, 28}
We could count out the values and find there are 26 of them.
That is a bit tedious. It's more efficient to use the rule below.
Rule:
If a set of consecutive integers starts at 'a' and ends at 'b', then there are b-a+1 elements to that set
Example: {7,8,9,10} has b-a+1 = 10-7+1 = 4 elements
I'll leave the formal proof to the reader.
There are b-a+1 = 28-3+1 = 26 numbers in the set {3, 4, 5, ..., 27, 28}
Consequently, there are 26 numbers in the set
{3*35, 4*35, 5*35, ..., 27*35, 28*35}
aka
{105, 140, 175, ..., 945, 980}
Answer: 26 numbers in common to both sets
--------------------------------------------------------
Another approach:
As mentioned earlier, 105 is the smallest number in set Z.
This is the first term of the arithmetic sequence.
Let a = 105
d = 35 is the common difference because we're dealing with multiples of 35
The nth term of the arithmetic sequence is
a(n) = a + d(n-1)
a(n) = 105 + 35(n-1)
a(n) = 105 + 35n-35
a(n) = 35n + 70
Plug in a(n) = 999 to reflect the largest three-digit number
Solve for n
a(n) = 35n + 70
999 = 35n + 70
35n = 999-70
35n = 929
n = 929/35
n = 26.542857 approximately
Plug in n = 26
a(n) = 35n + 70
a(26) = 35*26 + 70
a(26) = 980 which is the largest item of set Z
You should find that a(27) = 1015 which is too large.
It should be fairly self-explanatory at this point that there are 26 items in the set {a(1), a(2), a(3), ..., a(25), a(26)}
I.e. there are 26 items in the set {1, 2, 3, ..., 25, 26}
Answer: 26 numbers in common to both sets
|
|
|
