Question 1194603: Find the center, vertices, foci, ends of the latera recta and the equations of the directrices of the ellipse whose equation is y^2/36 + x^2/25 =1 and sketch the graph.
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52921)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
To make a sketch, go to free of charge calculator www.desmos.com,
print your equation there and obtain the plot in the next second.
Answer by Edwin McCravy(20065)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 Write as
Write as
 Compare to
Compare to
 which is an ellipse taller than it is wide
h=0, k=0, a=6, b=5 (a is larger than b in an ellipse)
From the center (h,k) = (0,0), go a=6 units up and down, to form
the major axis, and go b=5 units right and left, to form the minor axis.
The vertices are (h,k±a) = (0,a) and (0,-6)
The co-vertices are (h±a,k) = (-5,0) and (0,-5)
The major and minor axes are in green below: which is an ellipse taller than it is wide
h=0, k=0, a=6, b=5 (a is larger than b in an ellipse)
From the center (h,k) = (0,0), go a=6 units up and down, to form
the major axis, and go b=5 units right and left, to form the minor axis.
The vertices are (h,k±a) = (0,a) and (0,-6)
The co-vertices are (h±a,k) = (-5,0) and (0,-5)
The major and minor axes are in green below:
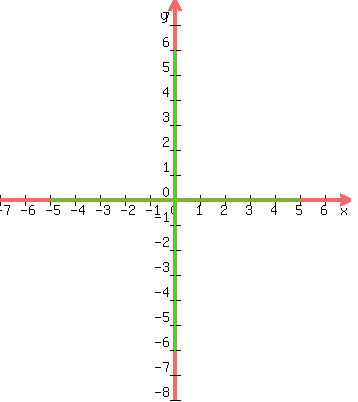 We sketch in the ellipse:
We sketch in the ellipse:
 We calculate c, the distance from Center to foCus.
We calculate c, the distance from Center to foCus.




 So the foci are (h,k±c) =
So the foci are (h,k±c) = 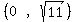 and and 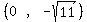 Draw the chords through them (in blue), which are
the latus recta:
Draw the chords through them (in blue), which are
the latus recta:
 We find the ends of the latus recta by substituting y=±√11 for y
in the equation of the ellipse and solving for x
We find the ends of the latus recta by substituting y=±√11 for y
in the equation of the ellipse and solving for x





 So the ends of the latus recta are
So the ends of the latus recta are
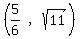 , ,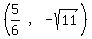 , ,
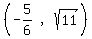 , ,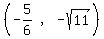 Edwin
Edwin
|
|
|