Question 1193656: Find the area of a triangle bounded by the y axis, the line f(x)=5-1/5x, and the line perpendicular to f(x) that passes through the origin
Answer by ikleyn(52932)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the area of a triangle bounded by the y axis, the line f(x)=5-1/5x, and the line
perpendicular to f(x) that passes through the origin
~~~~~~~~~~~~~~~~~
The line f(x) = 5 - 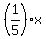 has x-intercept at
5 - has x-intercept at
5 - 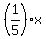 = 0 ----> 25 - x = 0 ----> x = 25.
So, the hypotenuse of the triangle lies on x-axis and goes from the origin to x= 25,
having the length of 25 units.
The perpendicular line is y = 5x (from analysis of slopes).
The intersection point of these two lines (x-coordinate) can be found as the solution to this equation
5 - = 0 ----> 25 - x = 0 ----> x = 25.
So, the hypotenuse of the triangle lies on x-axis and goes from the origin to x= 25,
having the length of 25 units.
The perpendicular line is y = 5x (from analysis of slopes).
The intersection point of these two lines (x-coordinate) can be found as the solution to this equation
5 - 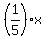 = 5x.
Simplifying, we get
25 - x = 25x
25 = 25x + x
25 = 26x ----> x = = 5x.
Simplifying, we get
25 - x = 25x
25 = 25x + x
25 = 26x ----> x = 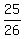 .
Then y-coordinate of the intercetion point is y = 5x = .
Then y-coordinate of the intercetion point is y = 5x = 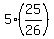 = =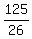 .
Now the area of the triangle is half the product of its hypotenuse, which is 25 units,
by .
Now the area of the triangle is half the product of its hypotenuse, which is 25 units,
by 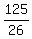 , which is y-coordinate of the intersection point, i.e. its distance from x-axis.
Therefore, the area of the triangle is
area = , which is y-coordinate of the intersection point, i.e. its distance from x-axis.
Therefore, the area of the triangle is
area = 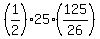 = =  = 60 = 60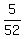 = 60.096 square units (rounded). ANSWER = 60.096 square units (rounded). ANSWER
Solved.
|
|
|