.
King David has two sets of numbers.
The first sets starts with 7 and follows a pattern of increasing by 6.
The second sets starts with 5554 and follows a pattern decreasing by 7.
How many numbers do the two sets have in common ?
~~~~~~~~~~~~~~~~~
First set is {a(n)} = { 7+6n | n= 0,1,2,3, . . . }. (1)
Second set is {b(m)} = { 5554-7m | m= 0,1,2,3, . . . }. (2)
For convenience, I wil present the second sequence in INCREASING order, too, by analogy with the first sequence.
Then the second sequence is {b(m) = { 3+7m | m= 0,1,2,3, . . . }.
(I chose a "3" as the starting point for the second sequence.
The value of "3" is the minimum positive number of the sequence (2),
and I start the sequece (2) from "3", since I am going to look for common terms with the sequense (1),
which starts from 7).
To start, I prepared Excel spreadsheet, which is shown below.
Sequence 2 Sequense 1
m b(m) n a(n)
----------------------------------------------------
0 3 0 7
1 10 1 13
2 17 2 19
3 24 3 25
4 31 4 31 (*)
5 38 5 37
6 45 6 43
7 52 7 49
8 59 8 55
9 66 9 61
10 73 10 67 (**)
11 80 11 73 (**)
12 87 12 79
13 94 13 85
14 101 14 91
15 108 15 97
16 115 16 103
17 122 17 109
18 129 18 115
19 136 19 121
20 143 20 127
21 150 21 133
22 157 22 139
23 164 23 145
24 171 24 151
25 178 25 157
26 185 26 163
27 192 27 169
28 199 28 175
29 206 29 181
30 213 30 187
31 220 31 193
32 227 32 199
33 234 33 205
34 241 34 211
35 248 35 217
36 255 36 223
37 262 37 229
38 269 38 235
39 276 39 241
40 283 40 247
41 290 41 253
42 297 42 259
43 304 43 265
44 311 44 271
45 318 45 277
46 325 46 283
47 332 47 289
48 339 48 295
49 346 49 301
50 353 50 307
51 360 51 313
52 367 52 319
53 374 53 325
54 381 54 331
55 388 55 337
56 395 56 343
57 402 57 349
58 409 58 355
59 416 59 361
60 423 60 367
61 430 61 373
62 437 62 379
63 444 63 385
64 451 64 391
65 458 65 397
66 465 66 403
67 472 67 409
68 479 68 415
69 486 69 421
70 493 70 427
71 500 71 433
72 507 72 439
73 514 73 445
74 521 74 451
75 528 75 457
76 535 76 463
77 542 77 469
78 549 78 475
79 556 79 481
80 563 80 487
81 570 81 493
82 577 82 499
83 584 83 505
84 591 84 511
85 598 85 517
86 605 86 523
87 612 87 529
88 619 88 535
89 626 89 541
90 633 90 547
91 640 91 553
92 647 92 559
93 654 93 565
94 661 94 571
95 668 95 577
96 675 96 583
97 682 97 589
98 689 98 595
99 696 99 601
100 703 100 607
By inspection, the first common term is the number 31: a( 4) = 7+6*4 = 31, b( 4) = 3 + 7*4 = 31 (marked by (*) in the Table).
The second common term is the number 73: a(11) = 7+6*11 = 73, b(10) = 3 + 7*10 = 73 (marked by (**) in the Table).
Notice that 73 - 31 = 42 = 6*7.
From now, it is clear that the common terms form an arithmetic progression
with the first term of 31 and the common difference of 42.
To find the number of such common terms, we divide the interval [31,5554] of the length (5554-30) = 5524
by equal intervals of the length 42: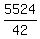 
= 131.52.
+-------------------------------------------------+
| So, we have 131 full interval, which means |
| that the number of common terms is 132. |
+-------------------------------------------------+
Thus the number of the common terms of sequences (1) and (2) is 132.
The greatest common term is 31 + 42*(132-1) = 5533.
ANSWER. There are 132 common terms. They form an arithmetic progression.
First common term is 31; the common difference is 42. The last common term is 31 + 42*131 = 5533.
Solved.
