SOLUTION: The perimeter of a rectangular bakery is 174 feet. The area is 1,782 square feet. What are the dimensions of the bakery?

Let x and y be the dimensions.


Then 

    x + y = 174/2 = 87      (1)    (half the perimeter)

    xy    = 1782            (2)    (the area)


From first equation, express y = 87-x and substitute into the second equation.

You will get single equation for unknown x


    x*(87-x) = 1782,

or

    x^2 - 87x + 1782 = 0.


Solve it using the quadratic formula.


     =  =  = .


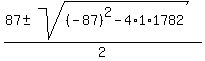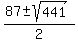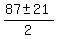Both roots are good,  x= 54 and x= 33.


First root x= 54 determines y = 87-54 = 33;

second root x= 33 determines y = 87-33 = 54.


So, the dimensions of the bakery are 33 and 54 feet.    ANSWER


CHECK  the area:  33*54 = 1782 square feet.   ! Precisely correct !