Question 1188652: A bacteria culture starts with 280 bacteria and grows at a rate proportional to its size. After 5 hours there will be 1400 bacteria.
A. What will the population be after 4 hours?
B. How long will it take the population to reach 2630? Give your answer accurate to 2 decimal places.
Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52778)   (Show Source):
You can put this solution on YOUR website! .
A bacteria culture starts with 280 bacteria and grows at a rate proportional to its size.
After 5 hours there will be 1400 bacteria.
A. What will the population be after 4 hours?
B. How long will it take the population to reach 2630? Give your answer accurate to 2 decimal places.
~~~~~~~~~~~~~~~~~~
Write the exponential growth function with arbitrary base b
B(t) =  ,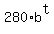
where "t" is the time in hours.
I use the multiplier 280, because it is the original number of bacteria at t = 0.
To find the base "b" value, write an equation as you read the problem
1400 =  ,
or
 = 
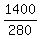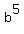5 = .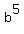
From here, you find b =  = 1.37973 (rounded).
So, the exponential growth function is
B(t) =  .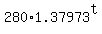
To answer first question, substitute t= 4 into the formula B(4) = 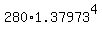 = 1015 (rounded).
To answer the second question, solve an equation
2630 = .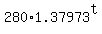
 = 
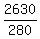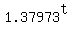9.3929 =
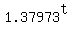log(9.3929) = t*log(1.37973)
t =  = 6.96 hours (about 7 hours).
Solved.
-----------------
To see many other similar and different solved problems on bacteria growth, look into the lesson
- Bacteria growth problems
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic "Logarithms".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! i think this means that it grows at a constant rate.
for example, something like 10% of its size, no matter what its size is.
the formula for that is f = p * (1 + r) ^ n
f is the future value.
p is the present value
r is the rate of growth per time period.
n is the number of time periods.
they state that it grows from 280 to 1400 in 5 hours.
the formula becomes 1400 = 280 * (1 + r) ^ 5.
divide both sides of this formula by 280 to get:
1400/280 = (1 + r) ^ 5.
take the fifth root of both sides of this equation to get:
(1400/280)^(1/5) = 1 + r.
subtract 1 from both sides of this equation to get:
(1400/280)^(1/5) - 1 = r
solve for r to get:
r = .379729661
that's the rate of growth per hour.
replace r in the original equation and solve for f to get:
f = 280 * (1 + .379729661) ^ 5 = 1400.
the rate is good.
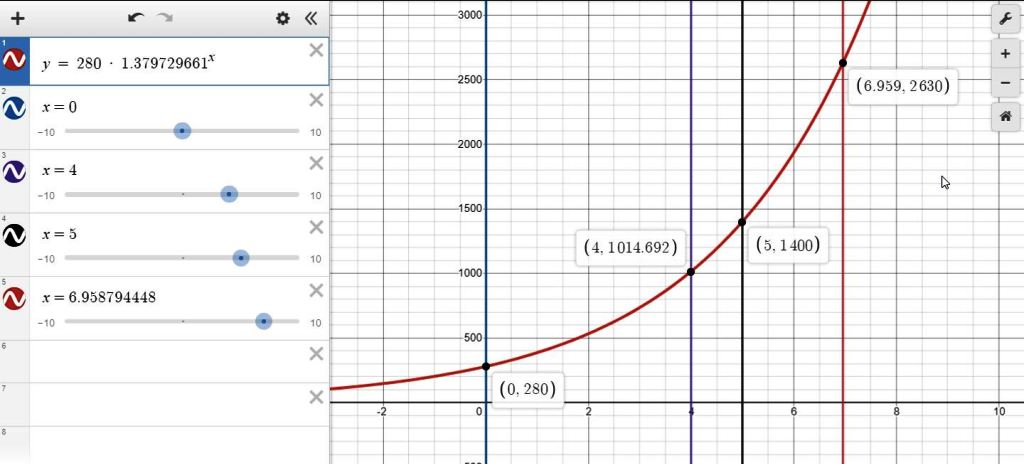
after 4 hours, the population will be:
f = 280 * (1 + .379729661) ^ 4 = 1014.691529.
1014.691529 is your solution to question a.
i'm not sure how they want you to round this so i left it as is.
to find how long it takes to grow to 2630, the formula becomes:
2630 = 280 * (1 + .379729661) ^ n
divide both sides of the equation to 280 and simplify the right side of the equation to get:
2630/280 = 1.379729661 ^ n
take the log of both sides of the equation to get:
log(2630/280) = log(1.379729661 ^ n)
since log(x^n) = n*log(x), this becomes:
log(2630/280) = n * log(1.379729661).
divide both sides of the equation by log(1.379729661) to get:
log(2630/280) / log(1.379729661) = n
solve for n to get:
n = 6.958794448.
confirm by replacing n in the original equation and solving for f to get:
f = 280 * 1.379729661 ^ 6.958794448 = 2630.
round to 2 decimal places to get n = 6.96
the equation can be graphed as shown below:
let me know if you have any questions.
theo
|
|
|
