Question 1187703: https://imgur.com/mLTjbMU In the diagram line AD = 2 cm, EF = 1 cm, and parallel segments are indicated. If the total area of the trapezoid is 105 cm^2, what is the area, in cm^2, of triangle AMN?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!
There is probably an easier way to solve this using ordinary geometry, but I'm not seeing it....
With the two sets of parallel lines, we know BE and FC are each 2cm.
With that, and knowing the area of ABCD is 105 cm^3, we can easily determine that the height of the trapezoid is 30cm.
Now we can use a strategy for solving the problem that is applicable to this and many similar problems. Since no angles are specified, the result must be independent of the angles, so we can make them any angles we want.
In particular, we can re-draw the figure with angle B a right angle, making the figure like this:
Now we can use coordinate geometry to find the equations of segments DE, AF, and AC and use their intersections to find that the coordinates of N and M are (2,10) and (2,18). (I leave it to you to do that much of the work.)
Then we see that triangle AMN has base length 8 and height 2, making its area (one-half base times height) 8.
ANSWER: The area of triangle AMN is 8 cm^3
NOTE: I worked the problem with another arbitrary angle B and obtained the same result; choosing the right angle made the computations far easier....
Thanks to tutor @ikleyn for showing a purely geometrical solution. In looking for that kind of solution, I wasn't seeing enough pairs of similar triangles.
On the other hand, note that my solution is useful to the student in demonstrating the powerful problem-solving technique of being able to re-draw the figure in a way that makes the problem easier to solve.
Answer by ikleyn(52778)  (Show Source):
You can put this solution on YOUR website! .
https://imgur.com/mLTjbMU
In the diagram line AD = 2 cm, EF = 1 cm, and parallel segments are indicated.
If the total area of the trapezoid is 105 cm^2, what is the area, in cm^2, of triangle AMN?
~~~~~~~~~~~~~~~~~~~~~~
From parallelogram ABED, we have BE = AD = 2 cm.
From parallelogram AFCD, we have FC = AD = 2 cm.
So, the base BC of the trapezoid ABCD is 2 + 1 + 2 = 5 cm long.
Hence, the altitude of this trapezoid is 105 cm^2 divided by 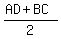 =  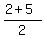=  = 3.5 cm,
which gives for the altitude 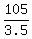 = 30 cm.
Next, triangles AND and FNE are similar (OBVIOUSLY) with the similarity coefficient 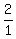 = 2;
So, their altitudes, drawn from their common vertex N to their parallel bases are 20 cm and 10 cm, in this order;
hence, the areas of these triangles are  = 5 cm^2 for triangle FNE and  = 20 cm^2 for triangle AND.
Further, triangles AMD and CME are similar with similarity coefficient  (as their bases AD and EC are in this ratio);
so, their altitudes, drawn from their common vertex M to their parallel bases AD and EC are  = 6*2 = 12 cm and 30-12 = 18 cm.
hence, the areas of these triangles are 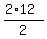 = 12 cm^2 for triangle AMD and  = 3*9 = 27 cm^2 for triangle CME.
Finally, the area of the triangle AMN is the difference of the area AND (20 cm^2) and the area AMD (12 cm^2), i.e. 20 - 12 = 8 cm^2.
ANSWER. The area of the triangle AMN is 8 cm^2.
Solved.
|
|
|
