.
A rectangle is inscribed in a circle of radius  . If the area of the rectangle is 16, find its dimensions.
. If the area of the rectangle is 16, find its dimensions.
~~~~~~~~~~~~~~~~~~~
Since the radius of the circle is  , its diameter is
, its diameter is  .
The diagonal of the rectangle is the diameter of the circle.
So, if x and y are the rectangle dimension, we have these two equations
x^2 + y^2 =
.
The diagonal of the rectangle is the diameter of the circle.
So, if x and y are the rectangle dimension, we have these two equations
x^2 + y^2 = 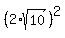 = 40, (1)
xy = 16. (2)
It implies
x^2 + 2xy + y^2 = 40 + 2*16 = 72
x^2 - 2xy + y^2 = 40 - 2*16 = 8,
or
= 40, (1)
xy = 16. (2)
It implies
x^2 + 2xy + y^2 = 40 + 2*16 = 72
x^2 - 2xy + y^2 = 40 - 2*16 = 8,
or
 = 72,
= 72,
 = 8.
Taking square roots from both sides of the equations, we get
x + y =
= 8.
Taking square roots from both sides of the equations, we get
x + y =  (3)
x - y =
(3)
x - y =  . (4)
By adding equations (3) and (4), you get 2x =
. (4)
By adding equations (3) and (4), you get 2x = 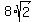 ; hence, x =
; hence, x = 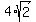 .
By subtracting equations (3) and (4), you get 2y =
.
By subtracting equations (3) and (4), you get 2y = 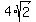 ; hence, y =
; hence, y =  .
ANSWER. The dimensions of the rectangle are
.
ANSWER. The dimensions of the rectangle are 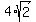 and
and  .
.
Solved.