Question 1187102: Triangle ABC has vertices A(-2,3), B(1,-3) and C(p,1). For how many values of p is the triangle isosceles?
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Triangle ABC has vertices A(-2,3), B(1,-3) and C(p,1).
For how many values of p is the triangle isosceles?
~~~~~~~~~~~~~~~~~~~~~
The solution by @MathLover1 is FATALLY INCOMPLETE.
There are several other, different isosceles triangles, that @MathLover1 missed/failed to find.
I came to bring the correct solution.
First, find the length of the side AB. It is (apply the distance formula)
d = 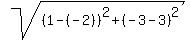 = = 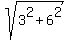 = =  = = 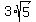 . .
Next, consider different cases.
Case AB = BC.
In this case, BC =  = = 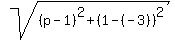 = = 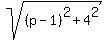 .
Squaring both sides, you get
45 = .
Squaring both sides, you get
45 =  ,
45 = ,
45 = 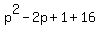
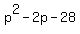 = 0 = 0
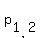 = = 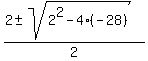 = = 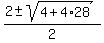 = = 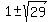 .
Thus, it gives two different real values for p, and, hence, two different isosceles triangles with AB = BC.
These two different isosceles triangles are shown in the Figure 1 below (blue lines). .
Thus, it gives two different real values for p, and, hence, two different isosceles triangles with AB = BC.
These two different isosceles triangles are shown in the Figure 1 below (blue lines).
 Figure 1. Two different triangles for case 1.
Case AB = AC.
In this case, AC =
Figure 1. Two different triangles for case 1.
Case AB = AC.
In this case, AC =  = = 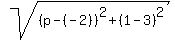 = = 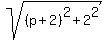 .
Squaring both sides, you get
45 = .
Squaring both sides, you get
45 = 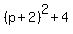 ,
45 = ,
45 = 
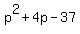 = 0 = 0
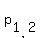 = = 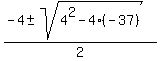 = = 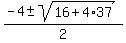 = = 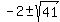 .
Thus, it gives two different real values for p, and, hence, two different isosceles triangles with AB = AC.
These two different isosceles triangles are shown in the Figure 2 below (blue lines). .
Thus, it gives two different real values for p, and, hence, two different isosceles triangles with AB = AC.
These two different isosceles triangles are shown in the Figure 2 below (blue lines).
 Figure 2. Two different triangles for case 2.
Figure 2. Two different triangles for case 2.
So, in my post I shown 4 possible isosceles triangles, missed by @MathLover1.
The fifth triangle is the one found in her post.
The ANSWER to the problem's question IS : 5 triangles are possible.
|
|
|