SOLUTION: a baking pan has an rectangular base 12 in by 8 in, the sides and ends of the pan slope outward, so that the upper edges measure respectively 13 1/2 in by 9 in. if the depth of the

Algebra ->  Customizable Word Problem Solvers  -> Geometry -> SOLUTION: a baking pan has an rectangular base 12 in by 8 in, the sides and ends of the pan slope outward, so that the upper edges measure respectively 13 1/2 in by 9 in. if the depth of the      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1181985: a baking pan has an rectangular base 12 in by 8 in, the sides and ends of the pan slope outward, so that the upper edges measure respectively 13 1/2 in by 9 in. if the depth of the pan is 2 in, find the amount of cake batter requires to fill the pan to 1/2 its depth
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13198) About Me  (Show Source):
You can put this solution on YOUR website!


------------------------------------------------------------------------

My visualization of the problem was faulty. The "pyramids" in the corners of the pan have rectangular bases, not triangular.

Furthermore, the problem is easier than I made it, because the 8x12 dimensions of the bottom of the pan and the 9x13.5 dimensions of the top make those two rectangles similar; and that means the problem can be solved using the idea of a truncated pyramid.

Thanks to tutor @ikleyn for providing a solution by that method.

-------------------------------------------------------------------------

UGLY problem.... But I finally decided to buckle down and tackle it.

For calculating the volume of the pan, it can be divided up into several pieces. For the purpose of this problem, we will express the volume of each piece as a function of h, the height/depth.

(1) The largest piece is a rectangular prism, dimensions (12)x(8)x(h).

Volume of rectangular prism: %2812%29%288%29%28h%29+=+96h.

(2) Next there are triangular prisms along each side of the pan.

The base of the pan is 8x12 inches. With the sloping sides of the pan, the dimensions of the top edge of the pan are 9x13.5 inches.

That means along the long side of the pan the lengths of the top and bottom edges differ by (9-8)/2 = 0.5 = 1/2 inches; and along the short side of the pan the top and bottom edges differ by (13.5-12)/2 = 0.75 = 3/4 inches.

But those are the "overlaps" for the full pan, with a depth of 2 inches. For solving this problem we will need to write those overlaps as functions of the depth h. So the overlap along the long edge, 1/2 inch when the depth is 2 inches, is (1/4)h. And the overlap along the short edge, 3/4 inch when the depth is 2 inches, is (3/8)h.

So we have two triangular prisms along the two long edges; the legs of the triangular base are h and (1/4)h, and the length is 12.

Volume of those two triangular prisms: %282%29%28%281%2F2%29%28h%29%28%281%2F4%29h%29%29%2812%29+=+3h%5E2

Similarly we have two triangular prisms along the two short edges; the legs of the triangular base are h and (3/8)h, and the length is 8.

Volume of those two triangular prisms: %282%29%28%281%2F2%29%28h%29%28%283%2F8%29h%29%29%288%29+=+3h%5E2

(3) Lastly, in each of the four corners of the pan we have a pyramid with height h and 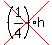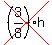cross%28bases%29 cross%28%281%2F4%29h%29 cross%28and%29 cross%28%283%2F8%29h%29 rectangular bases (1/4)h by (3/8)h.

Volume of the four pyramids: %284%29%28%281%2F3%29%28%28%281%2F4%29h%29%28%283%2F8%29h%29%29%29%28h%29+=+%281%2F8%29h%5E3

So the volume of whatever is in the pan as a function of the depth is

V%28h%29+=+96h%2B6h%5E2%2B%281%2F8%29h%5E3

We are to find the volume of the batter when the pan is filled to half its depth of 2 inches; so we need to evaluate this volume function for h=1.

V%281%29+=+96%2B6%2B1%2F8 = 102.125 cubic inches.

Note the volume of the full pan is V(2) = 192+24+1/2 = 216.5 cubic inches; the amount of batter to fill the pan to half its depth should be a bit less than half the full volume, so our answer of about 102 cubic inches is reasonable.

ANSWER: 102.125 cubic inches of batter will fill the pan to half its depth.

Answer by ikleyn(52778) About Me  (Show Source):
You can put this solution on YOUR website!
.
a baking pan has an rectangular base 12 in by 8 in, the sides and ends of the pan
slope outward, so that the upper edges measure respectively 13 1/2 in by 9 in.
if the depth of the pan is 2 in, find the amount of cake batter requires to fill
the pan to 1/2 its depth
~~~~~~~~~~~~~~~~~~~~ 


The base dimensions are 12 in by 8 in.


The upper edges measures are  13.5 inches  by  9 inches.


Dimensions at the 1/2 of the depth are (obviously)  12 + %2813.5-12%29%2F2 = 12.75 inches  by  8 + %289-8%29%2F2 = 8.5 inches.


It is not difficult to check that the shape under consideration is a pyramidal frustum.


Apply the formula for the volume of a pyramidal frustum 


     V = %28h%2F3%29%2A%28S%5Bt%5D+%2B+S%5Bb%5D+%2B+sqrt%28S%5Bt%5D%2AS%5Bb%5D%29%29.


Here h is the height of the frustum; S%5Bt%5D is the area of the top base face = 12.75*8.5 = 108.375 in^2;

S%5Bb%5D is the area of the bottom base face = 12*8 = 96 in^2.


So, the volume is


    V = %281%2F3%29%2A%28108.375+%2B+96+%2B+sqrt%28108.375%2A96%29%29 = 102.125 cubic inches.    ANSWER

Solved.

--------------

On the pyramidal frustum volume formula see the link

https://mathworld.wolfram.com/PyramidalFrustum.html

https://mathworld.wolfram.com/PyramidalFrustum.html


/////////////////


My answer differs from the answer by tutor @greenestamps.

It is because one formula in the solution by @greenestamps needs to be corrected.

This formula is for the volume of four pyramids in section (3) of the solution by @greenestamps

.

Its correct form is

%284%29%28%281%2F3%29%28%28%281%2F4%29h%29%28%283%2F8%29h%29%29%29%28h%29+=+%281%2F8%29h%5E3

without the factor 1%2F2.


With this correction, the solution by @greenestamps gives the same final answer of 102.125 in^3, as my solution.