Instead of doing it for you, I will do one exactly like it step-by-step.
Use it as a model to solve yours by. Here are the points I'll use instead:
The vertices of a triangle are P(-8,3), Q(-4,-7) and R(10,3).
Find the equation of the perpendicular bisector of the side QR.
That's the green line.
First we find the slope of QR using the slope formula:
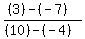
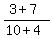
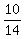
The perpendicular bisector is perpendicular, and the slope of any line
perpendicular to a line with a known slope is found by:
1. taking the reciprocal of that known slope.
2. giving it the opposite sign.
So the slope of the green perpendicular bisector is 
Since it bisects QR we find the midpoint of QR:
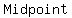
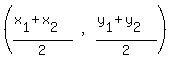
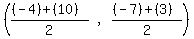
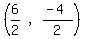
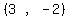To find the equation of the line we use the point-slope formula:
Find the slope of the median of the triangle that passes through point R.
That's the blue line, Which is the line from R to the midpoint of PQ
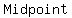
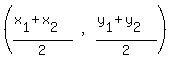
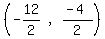
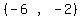We use the slope formula to find the slope of the line from that point to R.
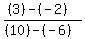
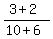
Find the slope of the altitude of the triangle that passes through point Q.That's the red line. (Watch out! This is a trick question!)
Since PR is a horizontal line, the altitude from Q to that line PR is
perpendicular to it, which means that it is vertical. A vertical line has
no slope, or sometimes we say the slope is not defined.
Now do your problem exactly the same way using your given points.
Edwin
