SOLUTION: The vertices of a kite are A (-3,1), B(0,5), C(4,2) and D(2, -9). Determine the lengths of the four sides of the kite. What do you notice? Determine the slopes of the dia

Algebra ->  Customizable Word Problem Solvers  -> Geometry -> SOLUTION: The vertices of a kite are A (-3,1), B(0,5), C(4,2) and D(2, -9). Determine the lengths of the four sides of the kite. What do you notice? Determine the slopes of the dia      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1179468: The vertices of a kite are A (-3,1), B(0,5), C(4,2) and D(2, -9).
Determine the lengths of the four sides of the kite. What do you notice?
Determine the slopes of the diagonals (from one corner to the other corner)
What do you notice?
Find the midpoint of the diagonal AC.
Find the equation of the diagonal BD.
Show the midpoint of AC lies on the equation of a line though BD.
Analyze the previous calculations and list as many properties of a kite as you can.
Answer by MathLover1(20849) About Me  (Show Source):
You can put this solution on YOUR website!

The vertices of a kite are
A (-3,1)
B(0,5)
C(4,2)
D(2,+-9)

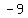Determine the lengths of the four sides of the kite. What do you notice?
the length of AB is:
AB=sqrt%28%280-%28-3%29%29%5E2%2B%285-1%29%5E2%29
AB=sqrt%283%5E2%2B4%5E2%29
AB=sqrt%2825%29
AB=5
the length of BC is:
BC=sqrt%28%284-0%29%5E2%2B%282-5%29%5E2%29
BC=sqrt%284%5E2%2B%28-3%29%5E2%29
BC=sqrt%2825%29
BC=5
the length of AD is:
AD=sqrt%28%282-%28-3%29%29%5E2%2B%28-9-1%29%5E2%29
AD=sqrt%285%5E2%2B%28-10%29%5E2%29
AD=sqrt%28125%29
AD=11.18

the length of CD is:
CD=sqrt%28%282-4%29%5E2%2B%28-9-2%29%5E2%29
CD=sqrt%28%28-2%29%5E2%2B%28-11%29%5E2%29
CD=sqrt%28125%29
CD=11.18
I noticed that the length of AB is equal to the length of BC, and the length of AD is equal to the length of CD

Determine the slopes of the diagonals (from one corner to the other corner)
What do you notice?
the diagonal AC lie on a line that contains vertices A and C
slope is m=%28y%5B2%5D-y%5B1%5D%29%2F%28x%5B2%5D-x%5B1%5D%29.......use A (-3,1) and C(4,2)
m=%282-1%29%2F%284-%28-3%29%29
m=1%2F%284%2B3%29
m=1%2F7
and BD lie on a line that contains vertices B(0,5) and D(2,+-9)
m=%28-9-5%29%2F%282-0%29
m=-14%2F2
m=-7
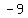=>I have noticed that slopes are negative reciprocal to each other which means the diagonals are perpendicular to each other

Find the midpoint of the diagonal AC.
A (-3,1) and C(4,2)
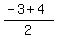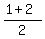M=(%28-3%2B4%29%2F2,%281%2B2%29%2F2)
M=(1%2F2,3%2F2)
Find the equation of the diagonal BD.
use m=-7 and point B(0,5), plug it in poit slope formula
y-y%5B1%5D=m%28x-x%5B1%5D%29
y-5=-7%28x-0%29
y-5=-7x
y=-7x%2B5
Show the midpoint of AC lies on the equation of a line though BD.
the midpoint of AC is M=(1%2F2,3%2F2)
y=-7x%2B5......substitute coordinates of the midpoint
3%2F2=-7%281%2F2%29%2B5
3%2F2=-7%2F2%2B10%2F2
3%2F2=3%2F2-> same, so the midpoint of AC lies on the equation of a line though BD