SOLUTION: Geometry. The length of a rectangle is 1 cm longer than its width. If the diagonal of the rectangle is 4 cm, what are the dimensions (the length and the width) of the rectangle?

Algebra ->  Customizable Word Problem Solvers  -> Geometry -> SOLUTION: Geometry. The length of a rectangle is 1 cm longer than its width. If the diagonal of the rectangle is 4 cm, what are the dimensions (the length and the width) of the rectangle?       Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 117871: Geometry. The length of a rectangle is 1 cm longer than its width. If the diagonal
of the rectangle is 4 cm, what are the dimensions (the length and the width) of the rectangle?
Found 2 solutions by ankor@dixie-net.com, solver91311:
Answer by ankor@dixie-net.com(22740) About Me  (Show Source):
You can put this solution on YOUR website!
The length of a rectangle is 1 cm longer than its width. If the diagonal
of the rectangle is 4 cm, what are the dimensions (the length and the width) of the rectangle?
:
Let x = the width
then
(x+1) = the length
:
The sides and the diagonal from a right triangle so we can use pythagorus here
a^2 + b^2 = c^2
:
In our problem a = x; b = (x+1); c = 4
:
x^2 + (x+1)^2 = 4^2
:
FOIL (x+1)(x+1)
x^2 + x^2 + 2x + 1 = 16
:
2x^2 + 2x + 1 - 16 = 0
:
2x^2 + 2x - 15 = 0; a quadratic equation
:
Solve for x using the quadratic formula; a=2; b=2; c=-15
x+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+
:
x+=+%28-2+%2B-+sqrt%28+2%5E2+-+4+%2A+2%2A+-15+%29%29%2F%282%2A2%29+
:
x+=+%28-2+%2B-+sqrt%284+-+%28-120%29+%29%29%2F%284%29+
:
x+=+%28-2+%2B-+sqrt%28124+%29%29%2F%284%29+; minus a minus is a plus
:
x+=+%28-2+%2B+11.1355%29%2F4; we only want the positive solution here
:
x+=+9.1355%2F4
:
x = 2.284 cm is the width
then
2.284 + 1 = 3.284 cm is the length
:
:
Check our solution:
2.284^2 + 3.284^2 =
5.2 + 10. 8 = 16 which is 4^2

Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
If you create a diagonal in a rectangle, then you have created a right triangle with the diagonal as a hypotenuse. Let's say the short leg of the triangle is x, and then the long leg (the long side of the rectangle) has to be x + 1. And we are given that the hypotenuse is 4 cm.
Pythagoras tells us that the sides and hypotenuse of a right triangle are related thus:

a%5E2%2Bb%5E2=c%5E2, or sqrt%28a%5E2%2Bb%5E2%29=c.

Replace a, b, and c with the values we are given:

sqrt%28x%5E2%2B%28x%2B1%29%5E2%29=4

Expand the binomial and combine terms under the radical

sqrt%28x%5E2%2Bx%5E2%2Bx%2Bx%2B1%29=4
sqrt%282x%5E2%2B2x%2B1%29=4

Square both sides:

2x%5E2%2B2x%2B4=16

Add -16 to both sides:

2x%5E2%2B2x-15=0

Use the quadratic formula
x+=+%28-2+%2B-+sqrt%28+2%5E2-4%2A2%2A%28-15%29%29%29%2F%282%2A2%29+
x+=+%28-2+%2B-+sqrt%28+124%29%29%2F4+
x+=+%28-2+%2B-+2sqrt%28+31%29%29%2F4+, so

x%5B1%5D+=+%28-1+%2B+sqrt%28+31%29%29%2F2+, or
x%5B2%5D+=+%28-1+-+sqrt%2831%29%29%2F2.

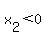x%5B2%5D+%3C+0 so we can exclude this answer because we are looking for a positive number length.

Since 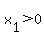sqrt%2831%29%3E5, x%5B1%5D%3E0, so x%5B1%5D+=+%28-1+%2B+sqrt%28+31%29%29%2F2+ is the answer we are seeking and is the width of the rectangle. The length of the rectangle is x%2B1, so the length must be %28%28-1+%2B+sqrt%28+31%29%29%2F2%29%2B1+=%281+%2B+sqrt%28+31%29%29%2F2%29

Hope this helps,
Happy Holidays,
John