Question 1166906: he Flying Insect Eliminator emits carbon dioxide and heat in a circular area with a radius of 38 feet. A fly is located 50 feet South and 62 feet West of the center of the Flying Insect Eliminator. The fly follows a straight-line path and exits the circular area at the Eastern most edge. A coordinate system can be imposed with (0,0) representing the center of the Flying Insect Eliminator as shown in the diagram below. The units of the coordinate system are in feet.
a) Find the location where the fly enters the circular area to the nearest tenth of a foot relative to the center of the Flying Insect Eliminator.
b) When tested, it was found that an insect needed to stay in the carbon dioxide and heat for at least five seconds to be zapped. If the fly has an average speed of 6.5 feet per second, Calculate the amount of time the fly is in the circular area to decide if it will live or die.
c) What is the closest distance the fly comes to the center of the Flying Insect Eliminator? Give your distance to the nearest foot.
Show all work!
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! i used a straight line distance and midpoint calculator and i used a straight line equation calculator to save myself the manual calculations to find the equation of a straight line and to find the midpoint of the straight line.
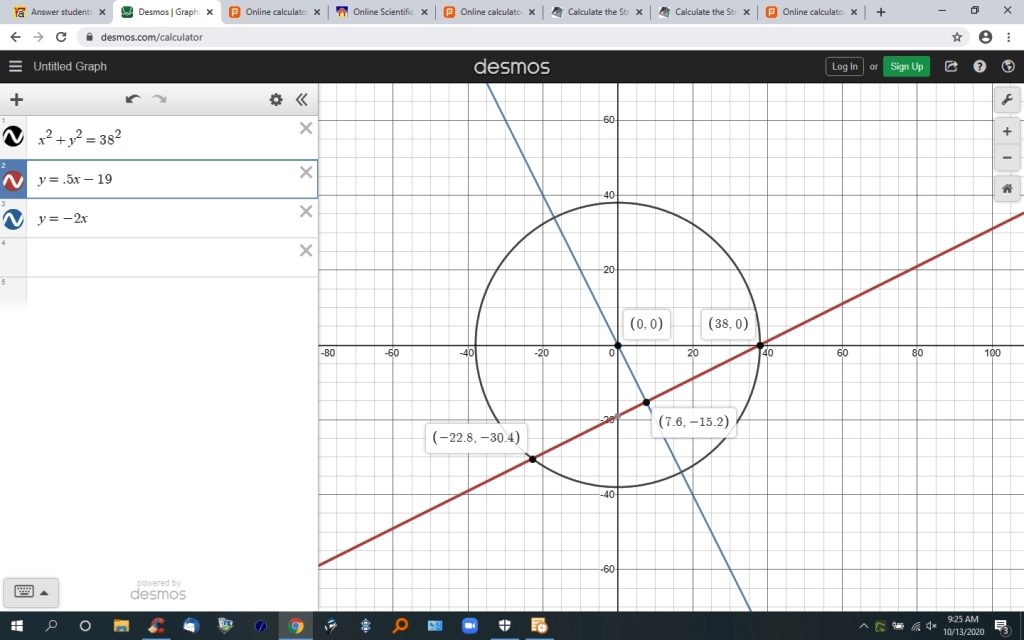
to begin with, i created the circle.
the equation for a circle that has the midpoint at the origin is:
x^2 + y^2 = r^2
in your problem, this becomes:
x^2 + y^2 = 38^2
i then graphed the circle on the desmos.com calculator.
this calculator is found at https://www.desmos.com/calculator.
the circle represents the center of the flying insect eliminator with a carbon dioxide and heat generating capable that goes out 38 feet from the center in a circular pattern.
the fly originates 50 feet south and 62 feet west of the center of the flying insect eliminator.
that makes the location of the fly on the graph at the point (-62,-50).
the fly will make a straight line path that goes through the flying insect eliminator and exit at the eastern-most end of it.
that makes the exit point for the fly from the flying insect eliminator at (38,0).
so the straight line starts at (-62,-50) and goes through (38,0).
the equation of that straight line is y=.5x-19
i graphed that on the desmos.com/calculator.
the fly enters the circle at the point (-22.8,-30.4) and exits the circle at (38,0).
the midpoint of that line segment is equal to the point (7.6,-15.2).
the line from that point to the point (0,0) has an equation of y = -2x.
i graphed that line on the desmos.com/calculator.
i then calculated the distance of that line segment between the point (0,0) and the point (7.6,-15.2)
that distance was equal to 16.99 feet.
i then calculated how long the fly was in the kill zone of the flying insect eliminator.
the distance through the circle was 67.98 feet.
the fly's rate of speed was 6.5 feet per second.
the fly was in the kill zone for 10.458461 seconds.
unfortunately, the fly never made it, since it died 5 seconds after entering the kill zone.
the distance that it traveled through the kill zone in 5 seconds was 5 * 6.5 = 32.5 feet.
it didn't even make it halfway through.
here's the graph.
there was a lot of manual calculations involved that i avoided by using online calculators that did the dirty work for me.
one of those calculators is the desmos.com calculator that can be found at https://www.desmos.com/calculator
another is the distance and midpoint calculator that can be found at https://planetcalc.com/8120/
another is the straight line equation calculator that can be found at https://www.mathsisfun.com/straight-line-graph-calculate.html
another is the solve equations simultaneously calculator that can be found at https://www.emathhelp.net/calculators/algebra-2/simultaneous-equations-solver/?s=y%3D.5x-19%2Cx%5E2%2By%5E2%3D38%5E2&v=
the problem was difficult to solve even with the use of the calculators.
without the use of the calculators, it would have been even more difficult.
but, it could be solved manually as well with a lot more effort.
anyway, your have your answers and you are free to duplicate them manually if you so desire.
your questions and solutions are shown below.
a) Find the location where the fly enters the circular area to the nearest tenth of a foot relative to the center of the Flying Insect Eliminator.
the fly enters the circle at the point (-62,50)
b) When tested, it was found that an insect needed to stay in the carbon dioxide and heat for at least five seconds to be zapped. If the fly has an average speed of 6.5 feet per second, Calculate the amount of time the fly is in the circular area to decide if it will live or die.
the fly is in the kill zone for 10.458461 seconds.
it didn't make it.
c) What is the closest distance the fly comes to the center of the Flying Insect Eliminator? Give your distance to the nearest foot.
the closest the fly gets to the center of the flying insect eliminator is 16.99 feet.
the equations you would need to solve this manually are:
equation of a circle with the center at (0,0):
x^2 + y^2 = r^2
r is the radius of the circle.
equation of a straight line:
y = mx + b
m is the slope
b is the y-intercept.
equation to find the the slope of y = mx + b
m = (y2-y1)/(x2-x1)
procedure to find b once you find m:
replace x and y with (x1,y1) or (x2,y2) to get:
y1 = m * x1 + b uses the point (x1,y1).
y2 = m * x2 + b uses the point (x2,y2).
equation of midpoint of a line segment:
midpoint = ( (x2 - x1)/2, (y2 - y1)/2 )
intersection points of a line and a circle:
two equations are:
x^2 + y^2 = r^2
y = mx + b
replace y in the first equation with its equivalent value of mx + b from the first equation and then solve the quadratic equation.
you will get two solutions.
one of them is the entry point and the other is the exit point.
intersection point of two lines:
y1 = m1x1 + b1
y2 = m2x2 = b2
solve simultaneously.
length of a line segment.
length = sqrt((x2 - x1)^2 + (y2 - y1)^2)
uses the points (x1,y1), (x2,y2) from the endpoints of the line segment.
good luck.
any problems with your calculations, let me know what you did and i'll see what went wrong.
any problems with understanding what i told you, let me know and i'll clarify as best i can.
|
|
|