Question 1159000: Four points on a circle divide it into four arcs, whose sizes are 52 degrees, 116 degrees, 100 degrees, and 92 degrees, in consecutive order. When extended, the chord that belongs to the 52-degree arc intersects the chord that belongs to the 100-degree arc, at a point P outside the circle. Find the size of angle P .
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Use the general theorem
The angle between two secants intersecting outside a circle has the measure
half the difference of the measures the arcs intercepted by the secants.
From the theorem, the measure of the angle P is 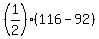 = 12 degrees. ANSWER = 12 degrees. ANSWER
Regarding this theorem, see the lesson
- The angle between two secants intersecting outside a circle,
in this site.
----------------------
On theory lessons on circles, their chords, secant and tangent lines, see
- A circle, its chords, tangent and secant lines - the major definitions,
- The longer is the chord the larger its central angle is,
- The chords of a circle and the radii perpendicular to the chords,
- A tangent line to a circle is perpendicular to the radius drawn to the tangent point,
- An inscribed angle in a circle,
- Two parallel secants to a circle cut off congruent arcs,
- The angle between two chords intersecting inside a circle,
- The angle between two secants intersecting outside a circle,
- The angle between a chord and a tangent line to a circle,
- Tangent segments to a circle from a point outside the circle,
- The converse theorem on inscribed angles,
- The parts of chords that intersect inside a circle,
- Metric relations for secants intersecting outside a circle
- Metric relations for a tangent and a secant lines released from a point outside a circle
- Quadrilateral inscribed in a circle
- Quadrilateral circumscribed about a circle
in this site.
On solved problems for circles, their chords, secant and tangent lines, see the lessons
- HOW TO bisect an arc in a circle using a compass and a ruler,
- HOW TO find the center of a circle given by two chords,
- Solved problems on a radius and a tangent line to a circle,
- Solved problems on inscribed angles,
- A property of the angles of a quadrilateral inscribed in a circle,
- An isosceles trapezoid can be inscribed in a circle,
- HOW TO construct a tangent line to a circle at a given point on the circle,
- HOW TO construct a tangent line to a circle through a given point outside the circle,
- HOW TO construct a common exterior tangent line to two circles,
- HOW TO construct a common interior tangent line to two circles,
- Solved problems on chords that intersect within a circle,
- Solved problems on secants that intersect outside a circle,
- Solved problems on a tangent and a secant lines released from a point outside a circle
- The radius of a circle inscribed into a right angled triangle
- Solved problems on tangent lines released from a point outside a circle
Also, you have this free of charge online textbook on Geometry
GEOMETRY - YOUR ONLINE TEXTBOOK
in this site.
The referred lessons are the part of this online textbook under the topic "Properties of circles, inscribed angles, chords, secants and tangents ".
Save the link to this online textbook together with its description
Free of charge online textbook in GEOMETRY
https://www.algebra.com/algebra/homework/Triangles/GEOMETRY-your-online-textbook.lesson
to your archive and use it when it is needed.
|
|
|