.
The given triangle is isosceles with congruent lateral sides of 15 inches long
and the base of 18 inches.
The altitude of this triangle drawn to the 18-inches side, divide this triangle in two right-angled triangles.
This altitude is one leg of these triangles, while the other legs are 18/2 = 9 inches long.
From the Pythagorean theorem, the length of the altitude is 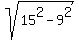 = 12 inches.
Then the area of the given triangle is
= 12 inches.
Then the area of the given triangle is  = 9*12 = 108 sq.inches.
Let the radius of the inscribed circle be r.
Now use the formula
area =
= 9*12 = 108 sq.inches.
Let the radius of the inscribed circle be r.
Now use the formula
area = 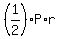 for the triangle, where P is the perimeter P of the triangle P = 15+15+12 = 42 inches.
The area of the triangle is 108 sq.inches.
Hence, 108 =
for the triangle, where P is the perimeter P of the triangle P = 15+15+12 = 42 inches.
The area of the triangle is 108 sq.inches.
Hence, 108 = 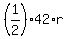 , which gives
r =
, which gives
r =  =
= 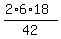 =
=  =
= 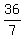 inches. ANSWER
inches. ANSWER