Question 1158992: All triangles and rectangles have circumscribed circles. Is this true for all kites, trape-
zoids, and parallelograms? Which quadrilaterals have circumscribed circles? Explain.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Not every polygon has a circumscribed circle. A polygon that does have one is called a cyclic polygon, or sometimes a con-cyclic polygon because its vertices are con-cyclic. All triangles, all regular simple polygons, all rectangles, all isosceles trapezoids, and all right kites are cyclic.
kites:
all 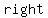 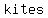 are are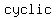 , the right kite is a convex quadrilateral and has two opposite right angles , the right kite is a convex quadrilateral and has two opposite right angles
all right kites are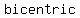 quadrilaterals (quadrilaterals with both a circumcircle and an in-circle) quadrilaterals (quadrilaterals with both a circumcircle and an in-circle)
trapezoid:
if the  is is 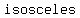 , the diagonals are of equal length, the two pairs of diagonally opposite angles will have equal sums, this sum being 180 degrees as the four angles must add to 360 degrees , the diagonals are of equal length, the two pairs of diagonally opposite angles will have equal sums, this sum being 180 degrees as the four angles must add to 360 degrees
this means that an 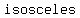 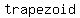 is a is a 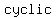 quadrilateral, and thus by definition can be circumscribed by a circle quadrilateral, and thus by definition can be circumscribed by a circle
parallelograms:
any parallelogram cannot be cyclic
for any quadrilateral to be cyclic the sum of the opposite angles should be 180 deg, so the parallelograms that can be cyclic are definitely a 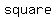 and a and a 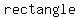
|
|
|