Question 1156829: Show that the lines y = 2x − 5 and −2x + 11y = 25 create chords of equal length when they intersect the circle x2 + y2 = 25. Make a large diagram, and measure the inscribed angle formed by these chords. Describe two ways of calculating its size to the nearest 0.1 degree. What is the angular size of the arc that is intercepted by this inscribed angle?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!
A good problem...
... from which you will learn nothing if we show you the complete solution.
So I'll give you some ideas and let you have the pleasure of solving the problem yourself.
The problem says the two chords of equal length form an inscribed angle. You can use that to check your work.
Solve the system of equations consisting of the circle and the first line; and similarly solve the system of the circle and the second line. You should find one point is a solution to both systems of equations, showing that the two lines intersect on the circle, forming an inscribed angle.
Having the coordinates of the points of intersection, use the distance formula to show that the lengths of the two chords are the same.
One of the points of intersection of the first line with the circle is (0,-5). You should be able to see that without doing any computations: the y-intercept of the first line is (0,-5), which is obviously a point on the circle.
Here is a graph:
I see two ways to determine the measure of the inscribed angle.
First way:
Draw the radii of the circle that form the central angle corresponding to the inscribed angle.
The measure of the central angle is 90 degrees (the third quadrant), plus the measure of a small angle in the second quadrant; you can determine the measure of that angle from the coordinates of the point of intersection in the second quadrant.
Then of course the inscribed angle is half the central angle.
Second way:
Since the two chords are the same length, the bisector of the inscribed angle passes through the center of the circle.
So the measure of the inscribed angle is twice the measure of the angle determined by the origin and the vertex of the inscribed angle.
I strongly recommend going through the calculations for both methods; it is always gratifying to show that you can get the same answer by two very different methods.
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
It is really nice problem, and it admits extraordinary beautiful solution, unexpected, elegant and without boring calculations.
But my method is totally different from the instructions in your post.
Also, my method is different from the @greenestamps approach.
It rarely happens to meet such beautiful problem. I will show you the solution,
and you can learn A LOT from it . . .
The idea of the solution is very simple:
+-------------------------------------------------------------------------------+
| Two chords in a circle are congruent (have the same length) if and only if |
| the chords are equally remoted from the center of the circle. |
+-------------------------------------------------------------------------------+
Indeed, if the circle has the radius R and a chord has the lenght L, then from Pythagorean theorem
you momentarily get this equation
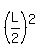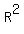 +  =  . (1)
where d is the distance from the center to the chord (the minimal distance, of course).
So, if two chords are given with the same lengths L, then from equation (1) they are equally remoted from the center.
And vice versa, if two chords are equally remoted from the center, then the formula (1) shows that in this case
their lengths are the same.
So, this statement is proved.
Hence, the only step to do is to check that the chords, defined by the given equations, are equally remoted
from the center of the circle.
There is a remarkable formula to calculate the distance from a given point to a given straight line in a coordinate plane.
Let the straight line in a coordinate plane is defined in terms of its linear equation
a*x + b*y + c = 0, (2)
where "a", "b" and "c" are real numbers, and let P = ( , ) be the point in the coordinate plane.
Then the distance from the point P to the straight line is equal to
d =  . (3)
Regarding this formula, see the lesson
The distance from a point to a straight line in a coordinate plane
in this site.
Your first straight line is y = 2x − 5, or, in the form (2), 2x - y - 5 = 0.
So, your coefficients are a= 2, b= -1, c= -5, and the coordinates of the point are = 0, = 0 (the center of the circle).
Substitute this data into the formula (3) to get the distance from the center to the line
d =  =  =  =  .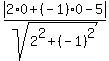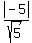
Your second straight line is −2x + 11y = 25, or, in the form (2), 2x - 11y + 25 = 0.
So, your coefficients are a= 2, b= -11, c= 25, and the coordinates of the point are = 0, = 0 (the center of the circle).
Substitute this data into the formula (3) to get the distance from the center to the second line
d =  =  =  = .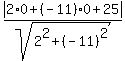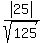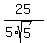
Thus you get the same distance d = for both lines.
Notice that the radius of the circle is 5 units, while the distance from the center (0,0) is d= , the lesser value,
so the lines really intersect the circle.
Hence, the chords are equally remoted from the center, and therefore, have equal lengths.
--------------
The solution is completed, and the statement is PROVED.
|
|
|
