Question 1156301: Let P(x)=x4 −2x3 −10x2 +6x+45
▪ Use the Rational Zero Theorem to list all the possible rational zeros. ▪ Then find all zeros exactly (rational, irrational, and imaginary).
Hint: Use the Rational Zero Theorem, a graphing calculator, and synthetic division if needed.
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Since the leading coefficient is 1, the Remainder theorem provides this list of possible zeros
(all of them are divisors of the constant term 45, in this case)
+/-1, +/-3, +/-5, +/-9, +/-15, +/-45.
Next, the plot below
 Plot y =
Plot y = 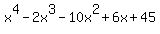 shows the root x= 3 of the multiplicity at least 2.
So, I divide
shows the root x= 3 of the multiplicity at least 2.
So, I divide 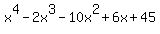 by by  , and I get the quotient , and I get the quotient 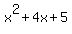 .
This quotient is a quadratic polynomial with negative discriminant, so it has no real roots.
Therefore, factoring over real numbers is .
This quotient is a quadratic polynomial with negative discriminant, so it has no real roots.
Therefore, factoring over real numbers is
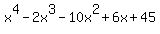 = = 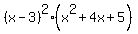 .
The quadratic polynomial x^2 + 4x + 5 has no rational roots.
It has no real roots, too, since its discriminant d = (-4)^2 - 4*1*5 = 16 - 20 = -4 is negative.
It has two complex roots .
The quadratic polynomial x^2 + 4x + 5 has no rational roots.
It has no real roots, too, since its discriminant d = (-4)^2 - 4*1*5 = 16 - 20 = -4 is negative.
It has two complex roots  = = 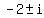 .
ANSWER. The roots of the given polynomial are x= 3 of the multiplicity 2 and
two complex roots .
ANSWER. The roots of the given polynomial are x= 3 of the multiplicity 2 and
two complex roots 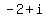 and and 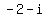 of the multiplicity 1 each. of the multiplicity 1 each.
Solved.
|
|
|