SOLUTION: A document is to contain 80 square centimetres of print. The margins at the top in bottom of the document are each 2 centimetres wide and the margins on each side are 3 centimetre

Algebra ->  Customizable Word Problem Solvers  -> Geometry -> SOLUTION: A document is to contain 80 square centimetres of print. The margins at the top in bottom of the document are each 2 centimetres wide and the margins on each side are 3 centimetre      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1155138: A document is to contain 80 square centimetres of print. The margins at the top in bottom of the document are each 2 centimetres wide and the margins on each side are 3 centimetres wide. What should be the dimensions (in centimetres) of print so that a minimum amount of paper is used?

Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.

They want you to minimize

    f(x,y) = (x+6)*(y+4)  under the condition  x*y = 80.  (1)

where x and y are the dimensions of the printed area.


In other words, from (1), you need to minimize

    f(x,y) = xy + 4x + 6y + 24 = 80 + 4x + 6y + 24 = 4x + 6y + 104.


From (1), you have  y = 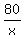80%2Fx, so the function f(x,y) takes the form

    g(x) = 4x + 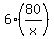6%2A%2880%2Fx%29 + 104 = 4x + 480%2Fx + 104.    (2)


So, you differentiate (2), and you get

    g'(x) = 4 - 480%2Fx%5E2.


Equate it to zero

    g'(x) = 0 = 4 - 480%2Fx%5E2.


So, to find x, you have this equation

    4x%5E2 = 480,

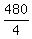    x%5E2 = 480%2F4 = 120

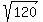     x = sqrt%28120%29 = 10.95 centimeters.


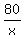Then y = 80%2Fx = 80%2Fsqrt%28120%29 = 7.30 cm.


Thus the dimension of the printed area are  10.95 cm width and 7.30 cm height.


The dimensions of the page are then  10.95 + 6 = 16.95 width and  7.30 + 4 = 11.30 cm height.

Solved.