SOLUTION: 689.What is the radius of the largest circle that you can draw on graph paper that encloses (a) no lattice points? (c) exactly two lattice points? (b) exactly one lattice point?

Algebra ->  Customizable Word Problem Solvers  -> Geometry -> SOLUTION: 689.What is the radius of the largest circle that you can draw on graph paper that encloses (a) no lattice points? (c) exactly two lattice points? (b) exactly one lattice point?      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1154420: 689.What is the radius of the largest circle that you can draw on graph paper that encloses
(a) no lattice points?
(c) exactly two lattice points?
(b) exactly one lattice point? (d) exactly three lattice points?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.

(a)  The radius of such a circle is less than  sqrt%282%29%2F2  units.

     But, although the radius is limited from above, there is NO the largest circle with such properties: 
     for any such a circle, there is another with the greater radius



(c)  Again, the radius in this case is limited from above by the value of sqrt%281%5E2+%2B+0.5%5E2%29 = sqrt%281.25%29 = sqrt%285%29%2F2 units.

     But, although the radius is limited from above, there is NO the largest circle with such properties: 
     for any such a circle, there is another with the greater radius,



(b)  The radius in this case is limited from above by the value of 1 unit,


     But . . . . . . . and so on . . . with the same refrain . . .


Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


(a) 0 lattice points

The center of the circle needs to be in the center of a square formed by four lattice points. The diagonal of the square has length sqrt%282%29; to contain no lattice points, the radius of the circle has to be less than sqrt%282%29%2F2.

Note the question as posed has no answer. We know the radius must be less than 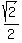sqrt%282%29%2F2%29; but there is no largest number less than sqrt%282%29%2F2.

(b) 1 lattice point

The center of the circle has to be a lattice point; and the radius has to be less than 1. Again there is no largest number less than 1; we only know the radius has to be less than 1.

(c) 2 lattice points

Put the center of the circle halfway between two adjacent lattice points. The center of the circle is then 1/2 unit from each of those two lattice points; its distance from each of the four closest other lattice points is 1/2 unit in one direction and 1 unit in the other direction, making a distance of 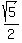sqrt%285%29%2F2.

So the radius can be anything less than 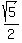sqrt%285%29%2F2.

(d) 3 lattice points

Consider this block of 9 lattice points:
   A   B   C

   D   E   F

   G   H   I


A circle centered at E with radius 1 would contain 5 lattice points -- B, D, E, F, and H.

If we move the circle very slightly diagonally from E towards I, we lose lattice points B and D, leaving us with the desired 3 lattice points.

The question then is how far can we move the center from E toward I and still have only 3 lattice points.

And the answer is that the limit is when the distances from the center of the circle and lattice points I and B (or D) are the same.

Let the center of the circle O be a distance x down and a distance x to the right of E. We want to know when the distances OB and OI are the same.

The length of OI is

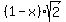
%281-x%29%2Asqrt%282%29

The length of OB is

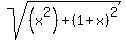
sqrt%28%28x%5E2%29%2B%281%2Bx%29%5E2%29

So

%281-x%29%2Asqrt%282%29+=+sqrt%28%28x%5E2%29%2B%281%2Bx%29%5E2%29

2%281-x%29%5E2+=+x%5E2%2B%281%2Bx%29%5E2
2%281-2x%2Bx%5E2%29+=+x%5E2%2Bx%5E2%2B2x%2B1
2x%5E2-4x%2B2+=+2x%5E2%2B2x%2B1
1+=+6x
x+=+1%2F6

So to have only 3 lattice points, the farthest we can move towards I from E is 1/6 of the distance.

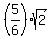And since the distance from E to I is sqrt%282%29, the radius of a circle which enclose exactly 3 lattice points has to be less than %285%2F6%29%2Asqrt%282%29.