Question 1153294: The area of a circle is 89.42 cm2. Which of the following most nearly gives the length of the side of a regular hexagon inscribed in the circle?
A. 4.22 cm
B. 5.33 cm
C. 5.89 cm
D. 6.12 cm
Found 3 solutions by MathLover1, ikleyn, MathTherapy:
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
From the figure, it is clear that, we can divide the regular hexagon into 6 identical equilateral triangles.
We take one triangle 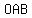 , with , with 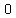 as the center of the hexagon or circle, & as the center of the hexagon or circle, &  as one side of the hexagon. as one side of the hexagon.
Let 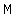 be mid-point of be mid-point of  , ,  would be the perpendicular bisector of would be the perpendicular bisector of  , angle , angle  ° °
Then in right angled triangle 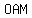 , side is , side is 

So, 
Therefore, 
Area of circle is,


if given that the area of a circle is  , we have , we have





so,
D. 6.12 cm -> should be 
Answer by ikleyn(52781)   (Show Source): (Show Source):
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! The area of a circle is 89.42 cm2. Which of the following most nearly gives the length of the side of a regular hexagon inscribed in the circle?
A. 4.22 cm
B. 5.33 cm
C. 5.89 cm
D. 6.12 cm
As stated, TOTALLY IGNORE the person who claims to LOVE MATH.
Area of THIS circle: 89.42 cm2
Area of ANY circle: πr2
We then get: πr2 = 89.42

r, or 
The RADIUS of the circle is the same length as the length of ANY one of the ISOSCELES sides of the 6 triangles of the INSCRIBED REGULAR HEXAGON!
|
|
|