SOLUTION: Given one large coin with 4.8 cm in diameter and many small coins with 1.5 cm in diameter. Determine the number of small coins that maybe arrange tangentially around the large coin

First determine the angle, at which you see the small coin from the center of the large coin.


For it, draw the segment from the center of the large coin to the center of the small coin.

The length of this segment is  4.8/2 + 1.5/2 = 6.3/2 = 3.15 cm.


Draw another segment from the center of the large coin, which is TANGENT to the small coin.

Also draw the radius of the small coin to the tangent point.


Then you get a right angled triangle, whose hypotenuse is 3.15 cm and the small leg is 1.5/2 = 0.75 cm.


Find an acute angle "a" measure of this triangle at the center of the large coin

    sin(a) = 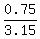 = 0.2381 (approximately).


Hence, the measure of angle "a" is

    a = arcsin(0.2381) = 0.24 radians.


Therefore, the "visibility angle" for a small coin is 2a = 2*0.24 radians = 0.48 radians.


Now, to find the number of small coins around the large coin, divide the full angle of  radians by 0.48 radians


    the number of small coins around the large coin = 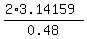 = 13.09 (approximately).


The last step is to round this value to the closest smaller integer.


ANSWER.  13 small coins.