Question 1135973: The measure of the exterior angles of a convex pentagon are consecutive integers. find the measure of each exterior angle.
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The sum of the exterior angles of any polygon equals 360°.
A pentagon has 5 sides and 5 vertices, so there are 5 exterior angles.
The exterior angles are consecutive integers, so they are
n°, (n+1)°, (n+2)°, (n+3)°, (n+4)°
Put plus signs between them and write = 360°, then solve the
equation for n. Then calculate the 5 exterior angles
Edwin
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
For any convex polygon, the sum of its exterior angles is equal to 360°.
So, you need to find 5 consecutive integer numbers, whose sum is equal to 360.
You can momentarily, immediately and instantly determine the middle of these 5 integer numbers: it is the number 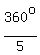 = 72°.
Indeed, if n is this middle integer number, then the sequence itself is
(n-2), (n-1), n, (n+1) and ((n+2)
with the sum (n-2) + (n-1) + n + (n+1) + (n+2) = 5n, which gives for the middle number n the expression and the value of
n = = 72°.
Indeed, if n is this middle integer number, then the sequence itself is
(n-2), (n-1), n, (n+1) and ((n+2)
with the sum (n-2) + (n-1) + n + (n+1) + (n+2) = 5n, which gives for the middle number n the expression and the value of
n = 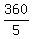 = 72.
Thus the five angles are 70°, 71°, 72°, 73° and 74°. ANSWER = 72.
Thus the five angles are 70°, 71°, 72°, 73° and 74°. ANSWER
Solved // mentally.
|
|
|