Question 1126088: Find the diameter of the largest circular pond that could fit in a triangular garden with verticies at (18,54),(-27,36),(27,-18, where a unit represents 1m
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
first use distance formula to find the length of the sides:
a triangular garden with vertices at
A=( , , ), ),
B=( , , ), ),
C=( , ,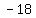 ) )
find AB:
AB=c ->
find BC:
BC=a ->
find AC:
AC=b ->
Here is a formula in terms of the three sides:
If the sides have length  , , , ,  , we define the semi-perimeter s to be half their sum, so , we define the semi-perimeter s to be half their sum, so  . .


Given this, the radius is given using the following:



Take the square root of this expression to find  . .

 meters meters
then, the diameter is  meters meters
|
|
|