Question 1123297: Seventeen lines drawn in a plane, with no 3 concurrent and no 2 parallel, divide the plane into closed regions(bounded on all sides) and open regions. The number of closed regions is?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Each group of 3 lines makes one triangle;
and vise versa, each such a triangle defines a group of 3 lines by an unique way.
So, there are 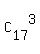 triangles.
Each group of 4 lines makes one quadrilateral;
and vise versa, each such a quadrilateral defines a group of 4 lines by an unique way.
So, there are triangles.
Each group of 4 lines makes one quadrilateral;
and vise versa, each such a quadrilateral defines a group of 4 lines by an unique way.
So, there are  quadrilaterals.
Each group of 5 lines makes one pentagon;
and vise versa, each such a pentagon defines a group of 5 lines by an unique way.
So, there are quadrilaterals.
Each group of 5 lines makes one pentagon;
and vise versa, each such a pentagon defines a group of 5 lines by an unique way.
So, there are 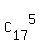 pentagons.
. . . . . . . . and so on . . . . . .
Each group of 16 lines makes one 16-gon;
and vise versa, each such a 16-gon defines a group of 16 lines by an unique way.
So, there are pentagons.
. . . . . . . . and so on . . . . . .
Each group of 16 lines makes one 16-gon;
and vise versa, each such a 16-gon defines a group of 16 lines by an unique way.
So, there are  16-gons.
Finally, all 17 lines together make 1 = 16-gons.
Finally, all 17 lines together make 1 = 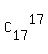 17-gon.
So, the number of all closed regions is the sum
S = 17-gon.
So, the number of all closed regions is the sum
S = 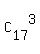 + +  + + 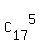 + . . . + . . .  + + 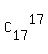 .
If you complement this sum with the terms .
If you complement this sum with the terms 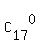 + + 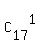 + C + C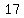 , you will get
S + , you will get
S + 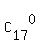 + + 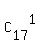 + C + C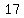 = = 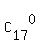 + + 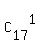 + C + C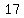 + + 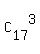 + +  + + 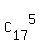 + . . . + . . .  + + 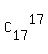 .
The long sum in the very right side is equal to .
The long sum in the very right side is equal to  . (*)
Therefore, the number S under the question is equal to
S = . (*)
Therefore, the number S under the question is equal to
S =  - ( - (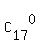 + + 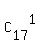 + C + C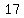 ) = ) =  - 1 - 17 - - 1 - 17 - 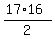 = =  - 1 - 17 - 136 = - 1 - 17 - 136 =  - 154. - 154.
Solved.
--------------------
In the solution, I used notations 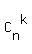 for the number of combinations of n items taken k at a time. for the number of combinations of n items taken k at a time.
I also used the formula (*) without proof.
This problem is of the Math circle level, so I assume that the person who will read this solution knows all these things.
If not, look into the lessons
- Introduction to Combinations
- PROOF of the formula on the number of Combinations
- Problems on Combinations
- OVERVIEW of lessons on Permutations and Combinations
- Binomial Theorem, Binomial Formula, Binomial Coefficients and Binomial Expansion
- Remarkable identities for Binomial Coefficients
- The Pascal's triangle
- Solved problems on binomial coefficients
- How many subsets are there in a given finite set of n elements?
in this site.
==============
For the reader who is interested in solution of such problems, the following info might be interesting.
I prepared 3 online textbook here, in the site www.algebra.com.
These textbooks are
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
Free of charge online textbook in GEOMETRY
https://www.algebra.com/algebra/homework/Triangles/GEOMETRY-your-online-textbook.lesson
Save this info in your archive as a text-file (.txt), and use it when it is needed.
|
|
|