Question 1117434: If each person occupies a 2ft x 2 ft area, how many people could you fit inside a triangular (equilateral)
concert area with a perimeter of 900 feet, and with t
he triangular height equal to 260 ft?
Found 3 solutions by josgarithmetic, MathTherapy, Alan3354:
Answer by josgarithmetic(39617)   (Show Source):
Answer by MathTherapy(10551)  (Show Source):
You can put this solution on YOUR website!
If each person occupies a 2ft x 2 ft area, how many people could you fit inside a triangular (equilateral)
concert area with a perimeter of 900 feet, and with t
he triangular height equal to 260 ft?
IGNORE this RUBBISH:  .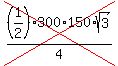
There's NO FRACTION of a PERSON! Try doing it yourself! You might be able to come up with something better than the RUBBISH above, posted by you-know-who!
The answer is an INTEGER!
Answer by Alan3354(69443)  (Show Source):
You can put this solution on YOUR website! If each person occupies a 2ft x 2 ft area, how many people could you fit inside a triangular (equilateral)
concert area with a perimeter of 900 feet, and with the triangular height equal to 260 ft?
-----------
300 ft sides --> height =~ 259.8 ft, less than 260
----
The number of 2 by 2 squares along an edge is limited to the distance parallel to the edge and 2 ft from it.
d = 300 - 2*2*tan(30) =~ 297.7 feet
--> 148 squares along an edge.
Each row above that is 4*tan(30) shorter.
The 2nd row is ~295.4 feet --> 147 squares, etc.
Using Excel --> 9603 people.
----------------------------
9603 times 4 = 38412 sq ft occupied of the total area of 38971 sq ft.
I don't think another arrangement would increase the number, but that would be difficult to prove.
|
|
|
