Question 1113151: In a circle with a diameter of 12 inches, a regular five-pointed star is inscribed. What is the area of that part not covered by the star? Please explain.
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! The regular five-pointed star,
and the circle with radius  where it is inscribed,
would look like this:
 We see that the star is a pentagon plus 5 isosceles triangles.
If you were given a formula to calculate areas of regular n-pointed stars inscribed in circles,
by all means use those formulas.
I think it is better not to use a formula if you do not have the formulas,
and are not able to deduce one quickly on the spot.
I can deduce one, but I prefer not to let formulas interfere with visualizing and understanding, so I will show a different approach.
We can figure out some angles:
The angle between the top point of the star and point 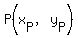 (the rightmost point of the 5-pointed star)
measures  ,
and the complementary angle,
the one between the positive x-axis and the red ray going through  ,
measures  .
With that we can calculate  as approximately  .
That is (in inches) the apothem of the pentagon, while the height (in inches) of the isosceles triangles is about
 .
Now we only need the  of the pentagon,
and then we would be able to calculate the area of the pentagon as
 ,
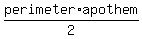and the area of the 5 triangles that make the points of the star as
 .
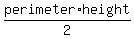There must be other formulas that we could look up,
but knowing that the angle marked with a green arc
(half of the 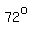 central angles of the pentagon),
measures 
we can calculate the length (in inches) of half a side of the pentagon as
That makes the perimeter of the pentagon approximately  .
The area of the pentagon (in square inches) is
 .
The area (in square inches) of the five triangles forming the tips of the star is
 .
The area (in square inches) of 5-pointed star is
 .
The area (in square inches) of the circle is  ,
so the area of that part not covered by the star is
|
|
|
