SOLUTION: Two regular quadrilateral vinyl tiles each of 1 ft sides overlap each other such that the overlapping region is a regular octagon. What is the area of the overlapping region?

Algebra ->  Customizable Word Problem Solvers  -> Geometry -> SOLUTION: Two regular quadrilateral vinyl tiles each of 1 ft sides overlap each other such that the overlapping region is a regular octagon. What is the area of the overlapping region?      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1112228: Two regular quadrilateral vinyl tiles each of 1 ft sides overlap each other such that the overlapping region is a regular octagon. What is the area of the overlapping region?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
FIRST A PICTURE (OR 2), TO VISUALIZE THE PROBLEM:
A regular quadrilateral is called a square.
The sketch below show red square tile
overlapping a green square tile
in the manner described in the problem.
The corners of the red tile are unsupported (not resting on the other tile).
Let me cut them out, so you can see the regular octagon.


CALCULATING THE AREA:
You could calculate the area of one square, and subtract
the area of the four corner triangles that are not overlapping the other square.
You could use the formula for the area of a regular polygon,
area=perimeter%2Aapothem%2F2 or area=%281%2F2%29%2Aperimeter%2Aapothem .
Either way, you need to know the length of a side of the octagon,
or the sides of those corner triangles.
Those corner triangles are isosceles right triangles,
meaning the two short sides (legs) have the same lengths.
Applying the Pythagorean theorem,
leg%5E2%2Bleg%5E2=hypotenuse%5E2 <--> 2leg%5E2=hypotenuse%5E2 <--> sqrt%282%29%0D%0A%2Aleg=hypotenuse <--> leg=hypotenuse%2Fsqrt%282%29
The side of the red square has a length of 1 foot,
so looking at one side of the red square and the attached triangles,
we see that leg%2Bhypotenuse%2Bleg=1foot .
If x is the length in ft of the side of the octagon (the hypotenuse of the triangles),
we can re-write the equations above into
x%2Fsqrt%282%29%2Bx%2Bx%2Fsqrt%282%29=1
x%2B2x%2Fsqrt%282%29=1
x%2Bx%2Asqrt%282%29=1
x%2A%281%2Bsqrt%282%29%29=1
x=1%2F%281%2Bsqrt%282%29%29
x=%28sqrt%282%29-1%29%2F%28%281%2Bsqrt%282%29%29%28sqrt%282%29-1%29%29
x=%28sqrt%282%29-1%29%2F%28%28sqrt%282%29%29%5E2-1%5E2%29
x=%28sqrt%282%29-1%29%2F%282-1%29
x=sqrt%282%29-1 .

USING AREA OF RED SQUARE MINUS AREA OF CORNER TRIANGLES:
The area of the red square, in square feet is
1%2A1=1 .
The corner triangles can be rearranged
(putting all four right angles together)
into a square of side x=sqrt%282%29-1 , with area
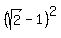%28sqrt%282%29-1%29%5E2 .
So the area of the octagon, in square feet, is


USING THE FORMULA FOR THE AREA OF A REGULAR POLYGON:
The length of a side of the octagon, in feet, is
x=sqrt%282%29-1 .
So, perimeter=8%28sqrt%282%29-1%29 .
The apothem of the octagon is
the distance from the center of the octagon to one of its sides,
it is also the distance from the center of the square to one of its sides,
and that is half of a square side 1%2F2 foot.
Substituting into the formula area=%281%2F2%29%2Aperimeter%2Aapothem , we get