Question 1111119: ABCD is a square with side length x cm. M and N are the midpoints of AD and CD respectively. The midpoints and point B make a triangle which is the shaded area. Find the ratio of the shaded to unshaded area.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! THE PICTURE:

THE FIFTH_GRADER'S SOLUTION:
If we connect M to the midpoint of BC,
and N to the midpoint of AB, we split the square into 4 smaller squares, each one being  of square ABCD. of square ABCD.
Joining 2 of those small squares we would get a rectangle
that is  of square ABCD. of square ABCD.
One of those 4 smaller squares
is divided into two equal triangular parts by diagonal MN,
so each of those two triangles is  of square ABCD. of square ABCD.
Triangle MND is  of square ABCD. of square ABCD.

The diagonal of a rectangle that is  of square ABCD of square ABCD
(such as diagonal MB),
divides the rectangle into two equal triangles.
Each of those triangles is  of square ABCD. of square ABCD.
Triangle ABM is  of square ABCD, and so is triangle NCB. of square ABCD, and so is triangle NCB.
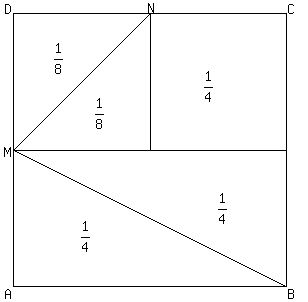
The unshaded area is triangles ABM + NCB + MND, and amounts to
 of the square. of the square.
So, the shaded area is
 of the square. of the square.
Obviously the ratio of shaded area to unshaded area is
 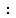 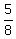 or or 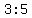
THE EXPECTED SOLUTION is probably as follows
As ABCD is a square with side length  cm", cm",
  . .
As "M and N are the midpoints of AD and CD respectively",
  . .
The unshaded area is made up of triangles  , , 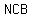 , and , and 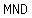 , ,
so its total area is easy to calculate.
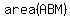  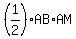  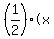 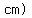    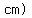  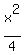  . .
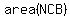  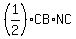  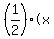 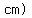    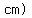  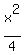  . .
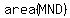  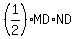  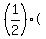  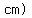    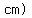  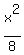  . .
   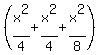   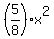 
Calculating the shaded area as the area of triangle MNB may seem difficult,
However,
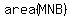  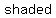   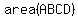   
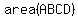  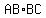  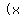 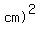   
So, 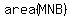  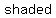     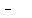 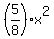   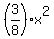  . .
The ratio of those two area values, both in  is is
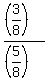  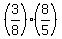   or or 
|
|
|