Question 1108215: 1. A triangular patch of grass in a park is bordered by walking paths. The longest path bordering the patch of grass measures 90 feet. The smallest path bordering the patch of grass measures 53 feet. The smallest angle formed by the paths bordering the patch of grass measures .
What is the measure of the largest angle of the triangular patch of grass?
Round your answer to the nearest tenth of a degree
Found 2 solutions by KMST, ikleyn:
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! We are considering a triangle whose longest side is 90 feet long,
and whose shortest side is 53 feet long.
That information does not identify what the triangle looks like.
Are we supposed to "make up" the missing information so as to make
the smallest angle as small as possible,
and the largest angle as large as possible?
The largest angle will be the one opposite the longest side.
The smallest angle will be the one opposite the shortest side.
The other angle will be the one opposite the other side.
Without any extra information, we can only look at some extreme cases,
and at cases in between.
CASE 1:
If the unknown side's length was 53 ft, we have two sides with that same length.
Talk about "the smallest path" or "the shortest side" does not sound quite right
if two paths/sides tie for the honor of being the smallest or shortest.
The triangle would look like this:
 . .
So,  and and  . .
The angles marked A tie for the smallest angle.
The other angle, measuring  , ,
is the largest angle in this triangle,
and the largest angle in a triangle where we could say that
the longest side measures 90ft and there is no side shorter than 53ft.
CASE 2:
If the unknown side's length was 90 ft,
the triangle would look like this:

So,  , ,  , ,
and  is the smallest angle in that triangle. is the smallest angle in that triangle.
The other two angles tie for the largest angle in that triangle,
measuring  . .
OTHER CASES:
The unknown side could length could also be between 53ft and 90ft,
and there could be other measures for the smallest angle.
For a triangle BCD, we could draw the 90-foot side, labeled as BC,
and draw an arc of radius 53ft centered at B.
The third vertex, D, would be somewhere on that arc,
not so close to C as to make side BD=53ft longer than side CD,
and not so far from C as to make side BC=90ft shorter than side CD.

Triangle 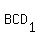 represents case 1, with angles measures represents case 1, with angles measures  , ,  , and , and 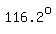 . .
Triangle 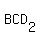 represents case 2, with angles measures represents case 2, with angles measures 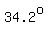 , , 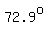 , and , and 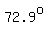 . .
Triangle  has has  tangent to the red arc, tangent to the red arc,
so the angle at  is a right angle, measuring is a right angle, measuring  , ,
and its other angles' measures are  and and  . .
The smallest angle in any other triangle that we could draw
satisfying the requirement of the problem would always be at C,
with  . .
The largest angle would always be at D,
with  . .
Answer by ikleyn(52936)   (Show Source): (Show Source):
|
|
|