Question 1105590: A curious card player wrote the nubmers 1,2,3,....,50 on fifty card and spread them out in front of him. First, he flipped all the cards over, so that they all were faced down. Next, he flipped all the cared that have even numbers. Then, he proceeded to flip all the cards with numbers divisible by 3, then, 4, 5, and so on up to 50. What is the sum of the numbers on the cards that were left faced down at the end ?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! If the cards were to be flipped only once, only the card with the number 1 would end face down. All the other cards would end up face up, the last one flipped being the one with the number 47. However, that would not be an interesting problem.
If multiple flips per card were allowed, the card with number 4 would be flipped face up with all the even number cards, but would get re-flipped to end face down when all the cards with numbers divisible by 4 were flipped. On the other hand, the cards with numbers 8 and 32 would be flipped an odd number of times and would end up face up.
So, which cards would end up face down?
The ones with numbers that have an even number of divisors greater than 1,
or in other words, the ones with an odd number of divisors.
How do we figure the number of divisors for a number?
We look at the prime factorization of the number, such as
 , ,  , ,  , or , or 
The number 1 has just 1 divisor, and that divisor is 1.
All other numbers up to 50 would have at most 3 different prime factors, because  . .
They would have a prime factorization of the form
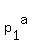 , with a total of , with a total of 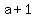 divisors, divisors,
all of the form 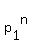 with with  an integer from an integer from  to to  , ,
or  , with , with 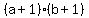 divisors, divisors,
or  , with , with 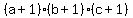 divisors. divisors.
For the number of divisors to be an odd number, all the exponents should be even numbers.
In the numbers up to 50, that only happens for
 , ,  , ,
 , ,  , ,  , ,
and  . .
The cards with those 5 numbers, and the card with number 1,
a total of  cards, would end up face down. cards, would end up face down.
|
|
|