.
You have these two equations
3x = 4y + 3k, (1)
2x +7y = 31k. (2)
Start writing them in the standard form:
3x - 4y = 3k, (3)
2x + 7y = 31k. (4)
Multiply eq(3) by 2 (both sides). Multiply eq(4) by 3 (both sides). You will get
6x - 8y = 6k, (5)
6x + 21y = 93k. (6)
Now subtract eq(5) from eq(6). The terms "6x" and "6x" will cancel each other, and you will get
21y + 8y = 93k - 6k ====> 29y = 87k ====> y = 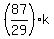 = 3k
Then from eq(2) 2x = 31k - 7*(3k) = 31k - 21k = 10k. Hence, x =
= 3k
Then from eq(2) 2x = 31k - 7*(3k) = 31k - 21k = 10k. Hence, x =  = 5k.
Now the ratio
= 5k.
Now the ratio  under the question is equal to
under the question is equal to 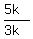 =
=  .
.
Solved.
In the solution, I applied the Elimination method.