.
Straight line perpendicular to 5x-y = 1 has an equation
5y + x = c, (1)
where c is some (arbitrary) constant.
Our original line has the slope 5; so, the perpendicular line has the slope  and has, therefore,
the equation y =
and has, therefore,
the equation y = 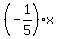 + c, which is the same as (1).
So, all you need to do is to determine the constant "c" in equation (1).
For it, notice that straight line (1) has x-intercept (c,0) and y-intercept (0,
+ c, which is the same as (1).
So, all you need to do is to determine the constant "c" in equation (1).
For it, notice that straight line (1) has x-intercept (c,0) and y-intercept (0,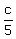 ).
It means, that your right-angled triangle has the legs of
).
It means, that your right-angled triangle has the legs of 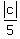 and |c| units long.
Then its area is
and |c| units long.
Then its area is 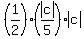 =
=  square units.
You need to have this area equal to 5 square units. It gives you an equation
square units.
You need to have this area equal to 5 square units. It gives you an equation
 = 5,
which implies
= 5,
which implies  = 50 and then c =
= 50 and then c = 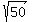 .
It means that your final equation under the question is
5y + x =
.
It means that your final equation under the question is
5y + x = 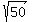 .
.
Solved.